Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 53
Para o elemento mostrado, determinar a variação para que a máxima tensão de tração seja igual ou inferior que .
Passo 1
O que a gente precisa fazer aqui é usar o Círculo de Mohr para descobrir o intervalo para no qual a tração seja no máximo igual a .
E como a gente faz isso? Vamos tentar montar esse círculo com as informações que a gente tem. Vamos listar:
- a tensão normal no eixo é positiva porque está saindo da seção e vale:
- a tensão normal no eixo é negativa porque está entrando na seção e vale:
- tensão máxima de tração:
- vamos considerar a tensão de cisalhamento como positiva como está na figura.
Bora começar!
Passo 2
Achando a coisinhas que a gente precisa para montar o Círculo de Mohr, vamos achar as coordenadas de , , o centro e o raio . Temos que:
E aqui a gente pode lembrar que .
Colocando essas coisas no Círculo:
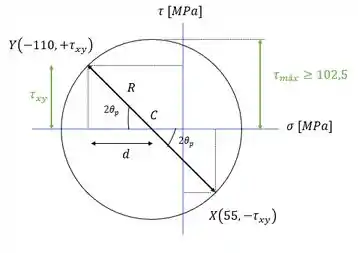
Passo 3
Agora a gente usa ele para calcular . Pela figura, lembramos que:
E usando as relações de triângulo retângulo:
Vamos usar o valor máximo de :
Aí, o intervalo fica:
Belezinha?