Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 42

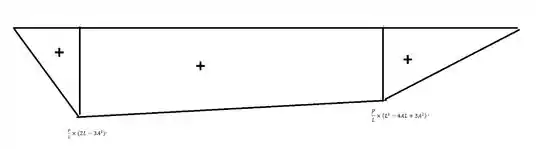
Usando o método da sec 7.4 resolver o problema 7.6

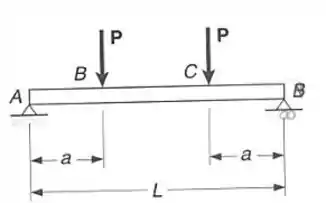
Passo 1

E ai gurizada tudo beleza? Espero que sim!!

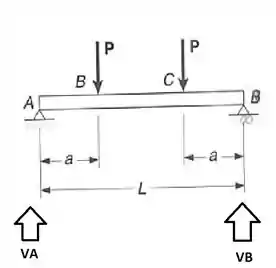
Vamos achar o VB primeiro vem comigo!!!

∑ M Z a = - P × a - P × 2 a + V B × L

V B = 3 P a L

Agora podemos achar VA

∑ F v = V A - P - P + V B = 0

∑ F v = V A - P - P + 3 P a L = 0

V A = P L × ( 2 L - 3 A )

Passo 2

Gurizadaaaaa agora que encontramos as reações partiu achar os cortantes! Vem cmg :D

Se considerarmos 0≤ x ≤a

Q   X = P L × ( 2 L - 3 A )

Se considerarmos A ≤x≤ (L – 2ª+A)

Q   X = P L × 2 L - 3 A - P L L

Q   X = P L × ( L - 3 A )

Se considerarmos (L-A) A ≤x≤ (L)

Q   X = P L × ( L - 3 A ) - P L L

Q   X = 3 P A L

Agora simmm podemos achar fazer o cortante

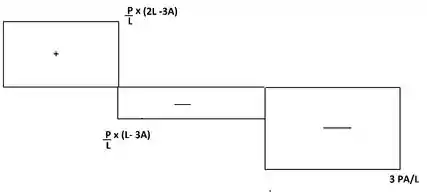
Passo 3

Vamos encontrar o momento ;)

Se considerarmos x=0 o m=0

Se considerarmos x=a o m(a)=   P L × 2 L - 3 A × a = P L × ( 2 L - 3 A ² )

Se x= (L-2A + A)

M   L - 2 A = P L × 2 L - 3 A × L - A - P   L - A × L L

M   L - 2 A = P L × 2 L 2 - 3 A L - 2 A L + 3 A 2 - P L   L ² - A L

M   L - 2 A = P L × 2 L 2 - 3 A L - 2 A L + 3 A 2 + P L   - L 2 + A L

M   L - 2 A = P L × 2 L 2 - 5 A L - 2 A L + 3 A 2 - L ² + A L  

M   L - 2 A = P L × L 2 - 4 A L + 3 A 2  

M (L)= 0

Agora sim podemos desenhar o diagrama do momento fletor

Resposta

M   L - 2 A = P L × L 2 - 4 A L + 3 A 2  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sabendo-se que σ a d m = 160M P a e τ a d m = 100M P a , selecionar o perfil I de abas largas que poderia ser usado para suportar o carregamento mostrado.
Sabendo-se que σ a d m = 16 5M P a e τ a d m = 100M P a , selecionar o perfil I de abas largas que poderia ser usado para suportar o carregamento mostrado.
Sabendo-se que σ a d m = 160M P a e τ a d m = 100M P a , selecionar o perfil I de abas largas que poderia ser usado para suportar o carregamento mostrado.
Determine as equações das curvas dos diagramas da força cortante e do momento fletor, para a viga com carregamento indicado. (Adotar a origem no ponto A.)
Usando o método da Sec 7.4, resolver o prob. 7.25