Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 34

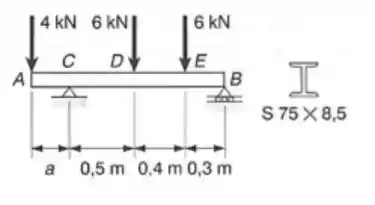
Determinar a) a distancia “a” para que o máximo valor absoluto do momento fletor na viga seja tão pequeno quanto possível B) a correspondente tensão normal, devido a flexão.

Passo 1

  1. E ai gurizada tudo beleza? Espero que sim!! Se liga que no item A ele pede para que a gente encontre a distância “a” na viga

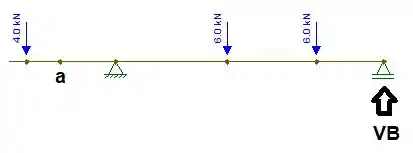
Então primeiramente vamos encontrar a reação VB, para isso vamos achar o momento , vem comigo!!

∑ M = F × d

∑ M Z c = - 4 a + 6 × 0,5 + 6 × 0,9 - 1,2 V B = 0

V B = - 3,33 a + 7

Um esboço do cortante seria , porém notem que ainda não achamos a distância “a”, mas agora vamos achar o momento em C , vem comigo

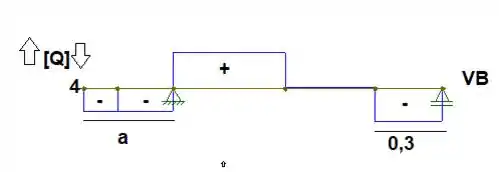
Lembrando que para acharmos o momento é

M = F × d

M c = 4 × 0,42 = 1,68   K N m   o u   1,68 × 10 6 N m m

Agora vamos fazer um esboço do momento para podermos encontrar finalmente o “a”

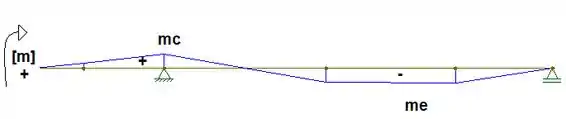
Vamos considera que...

m c = m e

4 a = 0,3   V B

So que VB achamos lá em cima, então iremos substituir aqui certo?

4 a = 0,3   × ( - 3,33   a + 7 )

a = 0,42   m

Passo 2

Aeeee gurizadaaa, agora partiu encontrar a tensão usando o perfil fornecido no enunciado

A inercia tu pode encontrar facilmente no livro, nos apêndices, lá no finalzinho 😊

Para calcularmos a tensão temos a seguinte equação

σ = M   x   ( h / 2 ) /   I z

σ = 1,68 × 10 6 × 38 1,05 × 10 6

σ = 60,8   M P a

Resposta

  1.   a = 0,42   m
  2. σ = 60,8   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas placas de cobertura, cada uma com 12,7m m de espessura, são soldadas a uma viga de perfil W 530 × 92 , como mostrado. Sabendo-se que l = 4,2 m e b = 250m m , determinar a máxima tensão normal em
Expressar o comprimento l de uma tira de madeira compensada do Exemplo 7.7, em termos de h ,L e h 0 , considerando que a viga deve ser de igual resistência, quando estiver suportando um carregamento u
Uma viga em balanço A B é de altura h constante e de largura b variável. Sabendo-se que a viga deve ser de resistência constante, expressar b em termos de b 0 ,x e L , se o único carregamento é: (a) u
Uma viga em balanço A B é de altura h constante e de largura b variável. Sabendo-se que a viga deve ser de resistência constante, expressar b em termos de b 0 ,x e L , se o único carregamento é: (a) u
Duas placas de cobertura, cada uma com 16m m de espessura, são soldadas a uma viga de perfil laminado W690 × 125 , como mostrado. Sabendo-se que l = 4,4 m e b = 30 0m m , determinar a máxima tensão no