Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 32

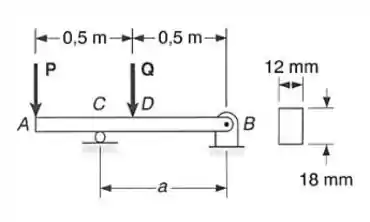
Sabendo-se que P=Q=530 N, determinar a) a distância para a, para que o máximo valor absoluto do momento fletor na viga seja tão pequeno quanto possível b) a correspondente tensão normal devido à flexão.

Passo 1

E ai gurizada tudo beleza? Espero que sim!!

  1. Partiu encontrar o momento, temos que definir a distância de A a C ,então para isso faremos a seguinte esquematização, veja ;)

    2. b =   1 - a = 1 - 0,8823 = 0,1339   m

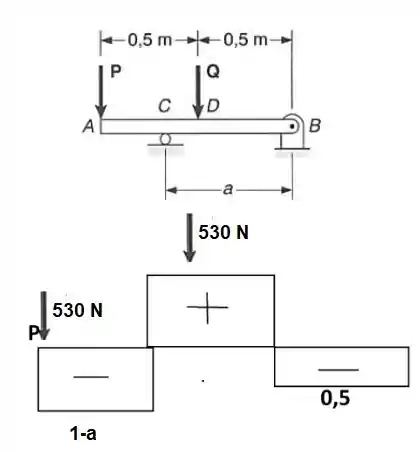
    Lembrando que para acharmos o momento é

    M = F × d

    M c = P × 0,1177 = 530 × 0,1177 = 70,967   N m

    M C = M D

    M = F × d

    P   1 - a = + V D × 0,5

    P - P a = + 530 a - 265 = ( P - a P 0,5 ) × a

    - 530 + 530 a + 530 a - 265 = ( 530 0,5 - - 530 a 0,5 ) × a

    - 795 + 1060 a = 1060 a - 1060 a ²

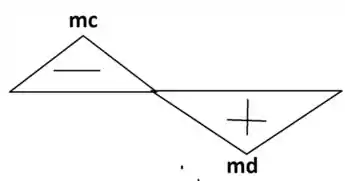
    a = 795 1060 = 0,866 m

    Passo 2

  2. Agora partiu encontrarmos a tensão? Vem comigo!!!

Buttt vamos achar a inercia antes conforme as medidas dos retângulos dados lá no enunciado

I z = b × h 3 12

I z = 12 × 18 3 12 = 5832   m m 4

I z = b × h 3 12

Para calcularmos a tensão temos a seguinte equação

σ = M   x   ( h / 2 ) /   I z

σ = 70,967 × 10 3 × 9 58322 m m 4

σ = 109,52   M P a

Resposta

  1.   0,866   m
  2. σ = 109,52   M P a
Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma viga A B é um sólido de revolução de diâmetro variável d . Para a porção A C da viga, expressar d , em termos de d 0 ,x e L , sabendo-se que a viga deve ser de igual resistência quando suporta o c
Duas placas de cobertura, cada uma com 12,7m m de espessura, são soldadas a uma viga de perfil W 530 × 92 , como mostrado. Sabendo-se que l = 4,2 m e b = 250m m , determinar a máxima tensão normal em
Duas placas de cobertura, cada uma com 16m m de espessura, são soldadas a uma viga de perfil laminado W690 × 125 , como mostrado. Sabendo-se que l = 4,4 m e b = 300m m , determinar a máxima tensão nor
Sabendo-se que σ a d m = 160M P a e τ a d m = 100M P a , selecionar o perfil I de abas largas que poderia ser usado para suportar o carregamento mostrado.
Para a viga com o carregamento mostrado, dimensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 860k P a .