Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 80
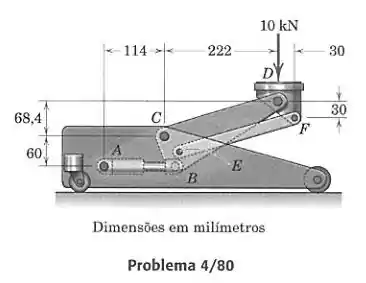
Os elementos de um macaco hidráulico estão mostrados na figura. Calcule a força no cilindro hidráulico devida à força suportada de 10 kN, como mostrado. Qual é a força no elo ?
Passo 1
Pra resolver esse problema, precisamos primeiro entender esse desenho difícil, identificando quais são os corpos que vamos usar para os diagramas de corpo livre e as forças. Primeiro vamos olhar a parte onde tá a força de 10 kN. Temos ali também o pino que deve fazer uma força e o pino também que faz uma força que deve ser na direção da barra :
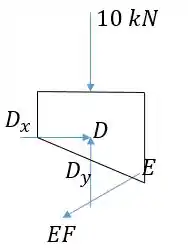
Agora olha para o ponto : todas as forças passam por ele, menos . Então é claro que tem que ser zero, porque se não fosse o momento em torno de não seria zero. Isso também resulta que a força em é para cima e vale 10 kN.
Passo 2
Agora queremos encontrar a força em . Se olharmos pro corpo , vemos que nele atuam as forças dos pinos (que é a própria força ), do pino (que já encontramos), do pino (zero) e do pino (desconhecida). Vamos então fazer nosso diagrama de corpo livre pra :
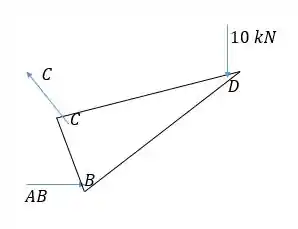
Desenhamos como se fosse uma força de compressão na barra . Agora com a equação do momento em torno de conseguimos encontrar , usando as distâncias dadas no enunciado:
Passo 3
Agora que temos 2 forças conhecidas e uma desconhecida, podemos fazer o equilíbrio das forças horizontais para encontrar :
Como :
Como a força na barra é de 300 N, a reação em será de 300 N.