Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.7 - Ex. 109
Desenvolva uma expressão para a projeção da força sobre a linha direcionada de a .
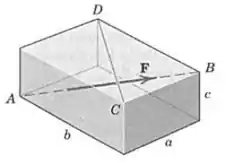
Passo 1
Para achar a nossa projeção vemos precisar escrever alguns vetores unitários: um na direção e outro na direção .
Para isso também vamos precisar definir um sistema de coordenadas:
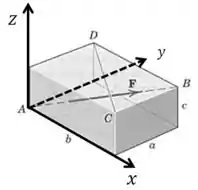
E então as coordenadas dos pontos são as seguintes:
Agora vamos escrever os vetores unitários nas direções de e :
Passo 2
Vamos usar o vetor unitário para encontrar a forma vetorial da força :
E o vetor unitário na direção é:
E agora para encontrar a projeção é só fazer o produto escalar desses dois vetores:
E lembre-se de que, no produto escalar, nós somamos os produtos de cada componente:
E essa é a expressão para a projeção .
Resposta
A projeção é dada por .
Exercícios de Livros Relacionados
Determine o ângulo θ entre a força e a linha A B .
Duas forças F 1 e F 2 atuam sobre o olhal. Se a força resultante F R tiver intensidade de 50N e ângulos de direção coordenados α = 110 ° e β = 80 ° , como mostrado, determine a intensidade de F 2 e se
Três forças atuam sobre o olhal. Se a força resultante F R tiver intensidade e direção como mostrado na figura, determine a intensidade e os ângulos de direção coordenados da força F 3 .
Determine os ângulos de direção coordenados de F 1 e F R :
Determine a intensidade e os ângulos de direção coordenados da força resultante em A .