Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 10

A empilhadeira mostrada na figura tem massa de 1.125 k g e é usada para elevar um caixote de massa m = 1,250 k g . A empilhadeira está se movendo para a esquerda com velocidade de 3 m / s quando os freios são acionados em todas as quatro rodas. Sabendo que o coeficiente de atrito estático entre o engradado e o garfo da empilhadeira é 0,30 , determine a menor distância que a empilhadeira pode utilizar para parar se o caixote não desliza e se a empilhadeira não tomba para a frente.

Passo 1

Considerem o esboço a seguir :D

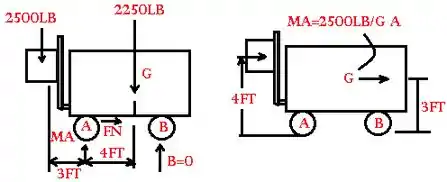
Passo 2

Presuma que a caixa não desliza e que o tombamento impende sobre A . ( B = 0 )

+ ∑ M A = ∑ M A e f f : 2500 l b   x   3 f t - 2250 l b   x   4 f t = - 2500 a g   x   4 f t - 2250 a g   x   3 f t 7500 - 9000 = - 10,000 + 6750 a g

a g = 0,09 ;     a = 0,09   x   ( 32,2 f t / s ² )   a = 2,884 f t / s ² →

Movimento uniformemente acelerado

v ² = v 0 2 + 2 a x ;       0 = ( 10 f t / s ) ² - 2   x   ( 2,884 f t / s ² ) x

Verifique se a caixa desliza. N = W

F = m a = W g a μ r e q = F N = a g = 2,884 f t / s ² 32,2 f t / s ²

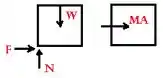
Resposta

x = 12,34 f t

μ r e q = 0,09 < 0,30 . A caixa não desliza.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Três barras, cada uma de massa de 4 kg, são soldadas juntas e unidas por pinos a duas hastes de conexão BE e CF. Desprezando o peso das hastes de conexão, determine a força em cada haste de conexão im
Um prato uniforme circular de massa de 3 kg é unido a duas hastes de conexão AC e BD de mesmo comprimento. Sabendo que o prato é solto a partir do repouso na posição mostrada na figura, determine (a)
Uma barra BC de 7,5 kg conecta-se a um disco centrado em A e na manivela CD. Sabendo que o disco é colocado para rodar a uma velocidade constante de 180 rpm, determine, para a posição mostrada na figu
No instante mostrado na figura, a velocidade angular das hastes de conexão BE e CF é de 6 rad/s no sentido anti-horário e está diminuindo a uma taxa de 12 rad/s2. Sabendo que o comprimento de cada has
Uma placa ABD e uma barra OB estão rigidamente conectadas e giram sobre a junta rotulada O com velocidade angular ω = ω x i ^ + ω x j ^ + ω z k ^ . Sabendo que v A =( 75m m / s ) i ^+( 350m m / s ) j