Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 16
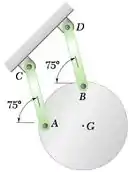
Um prato uniforme circular de massa de 3 kg é unido a duas hastes de conexão AC e BD de mesmo comprimento. Sabendo que o prato é solto a partir do repouso na posição mostrada na figura, determine (a) a aceleração do prato e (b) a tração em cada haste de conexão.
Passo 1
O exercício pede que a gente determine a) a aceleração do prato e (b) a tração em cada haste de conexão.
- Aceleração.
- Tensão em cada link.
Passo 2
Resposta
Exercícios de Livros Relacionados
Um disco de 100m m de raio gira à taxa constante ω 2 =4r a d/ s em torno de um eixo apoiado em uma estrutura presa a uma barra horizontal que gira a uma taxa constante ω 1 = 5r a d/ s . Sabendo que θ
Um cano de canhão de comprimento O P =4m está montado sobre uma torre blindada do modo mostrado na figura. Para manter o cano com a mira em um alvo móvel, o ângulo azimutal β é aumentado a uma taxa d
No sistema de engrenagens planetárias mostradas na figura, as engrenagens A e B estão rigidamente conectadas entre si e giram como uma unidade em torno do eixo inclinado. As engrenagens C e D giram co
Uma roda de 30 mm de raio é montada sobre um eixo OB de comprimento de 100 mm. Ela rola sem deslizar sobre o piso horizontal e seu eixo é perpendicular ao plano da roda. Sabendo que o sistema gira em
Várias barras estão soldadas juntas para formar um braço guia robótico mostrado na figura que é preso a uma junta rotulada em O. A barra OA desliza na ranhura reta inclinada enquanto a barra OB desliz