Enunciado
Mecânica e Resistência dos Materiais - Beer - Dinâmica- Ed: 9º - Capítulo 16.Problemas - Ex. 17
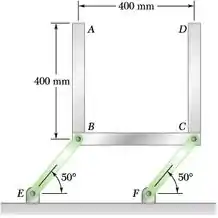
Três barras, cada uma de massa de 4 kg, são soldadas juntas e unidas por pinos a duas hastes de conexão BE e CF. Desprezando o peso das hastes de conexão, determine a força em cada haste de conexão imediatamente depois do sistema ser liberado do repouso.
Passo 1
O exercício pede que a gente encontre a força em cada haste de conexão imediatamente depois do sistema ser liberado do repouso.
O centro de massa do ABCD está em G
Passo 2
Realizando o momento em B temos:
Resposta
Exercícios de Livros Relacionados
No sistema mostrado na figura, o disco A é livre para girar sobre a barra horizontal AO. Considerando que o disco B é estacionário ( ω 2 =0 ) e que o eixo OC gira com velocidade angular constante ω 1
No sistema mostrado na figura, o disco A é livre para girar sobre a barra horizontal AO. Considerando que Considerando que o eixo OC e o disco B giram com velocidades angulares constantes ω 1 e ω 2 re
No Problema 15.192, determine (a) a velocidade do ponto A, (b) a aceleração do ponto A.
O braço BCD em forma de L gira em torno do eixo z com uma velocidade angular constante ω 1 de 5r a d/ s . Sabendo que o disco de 150m m de raio gira em torno de BC com uma velocidade angular constante
Um disco de 100 mm de raio gira à taxa constante ω 2 = 4r a d/ s em torno de um eixo apoiado em uma estrutura presa a uma barra horizontal que gira à taxa constante ω 1 = 5r a d / s . Para a posição m