Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 43
45. O encanamento está sujeito à força de . Determine o momento dessa força em relação ao ponto A.
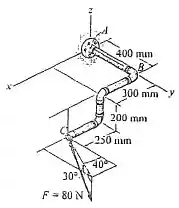
Passo 1
Para fornecer o resultado como o enunciado pede precisamos calcular o momento da força F usando o produto vetorial que é dado da seguinte maneira:
Onde:
representam as coordenadas do vetor que vai da origem da rotação até o ponto de aplicação da força;
são as componentes da força aplicada.
O vetor mencionado acima pode ser visto na figura abaixo.
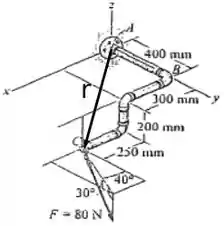
Para saber as coordenadas desse vetor, basta olhar a figura e ver quanto você tem que andar para cada direção para chegar ao ponto de aplicação da força, logo:
Passo 2
Mas antes de começar a usar esse método, temos que notar que a nossa força não está expressa em forma cartesiana, mas como o problema nos fornece os ângulos de inclinação do vetor força, podemos decompô-lo em suas componentes em x, y e z.
A componente em z é dado por:
Você pode ter se perguntado o porquê daquele sinal de menos, isso é simples, basta analisar a figura que você irá perceber que a componente z da força aponta para baixo, por isso o sinal.
Para analisar as componentes x e y da força, primeiro vamos projetar essa força do plano xy, para depois decompô-la em x e em y.
Assim essa força no plano xy é dada por:
Agora vamos achar a componente em x:
A componente em y é:
Passo 3
Agora que já obtemos tudo que precisávamos, vamos calcular o momento em relação ao ponto A.
Resposta
Assim o momento em relação ao ponto A expressado como vetor cartesiano é dado por: