Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 7.Problemas - Ex. 12
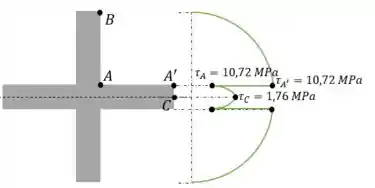
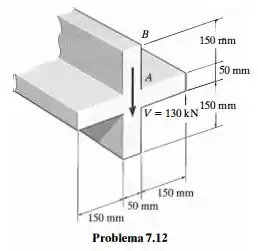
A escora está sujeita a um cisalhamento vertical . Construa um gráfico da intensidade da distribuição de tensão de cisalhamento que age na área da seção transversal e calcule a força de cisalhamento resultante desenvolvida no segmento vertical .
Passo 1
Fala ai galerinha bonita, tudo belejóia com vocês?
Saca só, nesse exercício aqui o enunciado nos diz que a escora está sujeito a um cisalhamento vertical . Sabendo disso, o enunciado nos pede para construir um gráfico da intensidade da distribuição de tensão de cisalhamento que age na área da seção transversal e calcular a força de cisalhamento resultante desenvolvida no segmento vertical .
Belezoca, então podemos começar esboçando um diagrama com a força representada como:
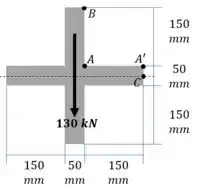
Primeiro vamos começar calculando o momento de inércia da seção. Depois vamos calcular as tensões sobre A, A’ e C. Com isso poderemos gerar o gráfico de tensão de cisalhamento.
Mas para definir o valor da força sobre uma região, precisamos integrar a equação . E pra isso precisamos definir uma equação para o momento estático, e depois aplicar a integração na equação 7.3.
Passo 2
Iradoso, então calculando o momento de inércia:
Logo:
Passo 3
Olhe a figura abaixo. Nosso interesse é calcular os momentos estáticos no ponto A, A’ e C.
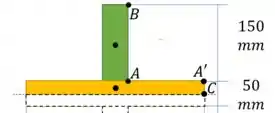
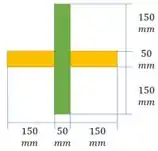
O momento estático no ponto A e A’ são o mesmo, e iguais ao demarcado em verde:
O momento estático no ponto C é dado pela soma da região verde e amarela:
Passo 4
Agora podemos calcular as tensões em cada ponto:
No ponto :
No ponto A’ temos um aumento da base :
No ponto C temos um aumento no momento estático:
Passo 5
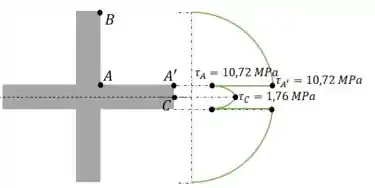
Com as tensões calculadas podemos gerar o gráfico da tensão de cisalhamento. Já sabemos algumas coisas: a primeira é que o comportamento da tensão é uma parábola. E segundo que nas extremidades da seção a tensão é zero.
Então a tensão parte do zero no ponto B e cresce até o ponto A. No ponto A para o A’ há uma mudança na espessura da seção, gerando uma queda repentina no gráfico. Após isso o gráfico continua crescendo até atingir o centroide.
Como a seção é simétrica, após o centroide a tensão é espelhada:
Passo 6
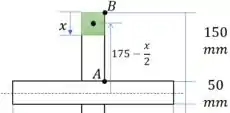
Agora vamos calcular a força que atua sobre a aba AB. Começamos definindo uma função para o momento estático. Observe a figura, e perceba como o momento estático cresce a partir de B até atingir o ponto A. Perceba também que à medida que a área verde aumenta, o seu centroide muda de posição.
Passo 7
Bem, sabemos por definição que tensão é força sobre área. Em termos infinitesimais:
Sabemos que a tensão de cisalhamento é dada por:
Isolando :
Perceba que a área da seção é quadrada. Em outras palavras:
Substituindo o valor de temos:
Simplificando:
Aplicando a integral, com os limites sendo o próprio tamanho da haste AB:
Resolvendo:
Substituindo os valores:
O resultado é:
Resposta
