Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas Revisão - Ex. 145

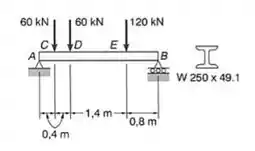
Resolver o P r o b . 5.14 , considerando que a carga vertical de 120   k N é removida.

Passo 1

Fala aí pessoal, nosso objetivo aqui são dois, determinar a máxima tensão normal que age no meio da nossa seção, e também a nossa máxima tensão cisalhante no mesmo ponto. Sabemos que nas vigas vamos ter que calcular as tensões pelas seguintes equações:

  • Tensão cisalhante devido o cortante

    • τ = V Q I b

    Em que:

    V = c o r t a n t e   a g i n d o   n a   s e ç ã o  

    Q = m o m e n t o   e s t á t i c o  

    I = m o m e n t o   d e   i n é r c i a  

    b = e s p e s s u r a   d a   r e g i ã o   q u e   d e s e j a   s e   s a b e r   a   t e n s ã o  

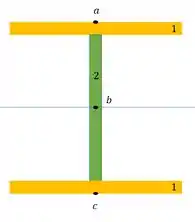
    Sabemos que a máxima tensão cisalhante vai ocorrer onde a LN passa, como a nossa seção é simétrica, sabemos que será bem no eixo de simetria, sendo assim, podemos definir o seguinte par aa tensão cisalhante:

    b = t w  

  • Tensão normal devido ao momento fletor.

σ = - M y I

Em que:

M = M o m e n t o   f l e t o r   a g i n d o  

y = d i s t â n c i a   d a   L N   a t é   o   p o n t o   m a i s   d i s t a n t e   d e l a   n a   v e r t i c a l = 40   m m    

I = m o m e n t o   d e   i n é r c i a  

Sabendo as fórmulas, podemos seguir em frente, vamos nessa?

Passo 2

Sabemos que a seção e suas características são dadas por:

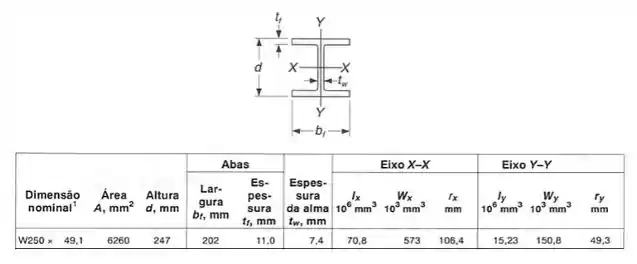
Como a viga está na vertical, podemos usar a seguinte relação:

I x x = I = 70,8   .   10 6   m m 4

A = 6260   m m 2

b = t w = 7,4   m m

y = d 2 = 247 2 = 123,5   m m

Agora, com relação a geometria, só falta o momento estático, e para isso precisamos ver a parte superior na nossa seção:

Q = A 1 y 1 + A 2 y 2   = 2222   .     118 + 832,5   .   56,25

Q = 309024,125   m m 3

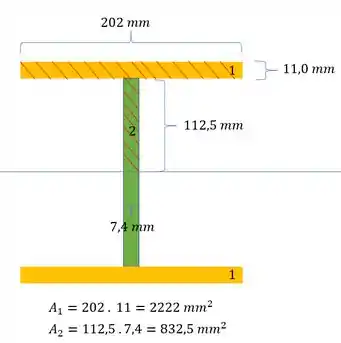
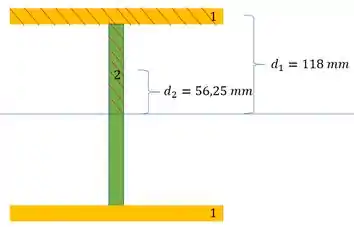
Agora tudo referente a geometria já temos, agora só precisamos calcular os esforços na nossa seção:

Passo 3

Vamos ao calculo dos esforços no meio da nossa seção, e para isso precisamos desenhar o nosso diagrama de cortantes e momentos fletores.

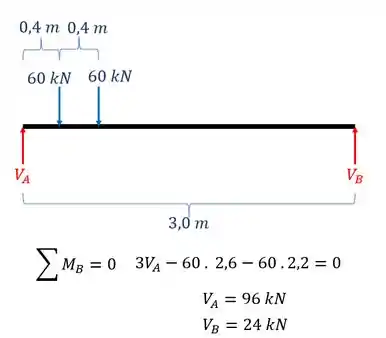
  • Esforço cortante

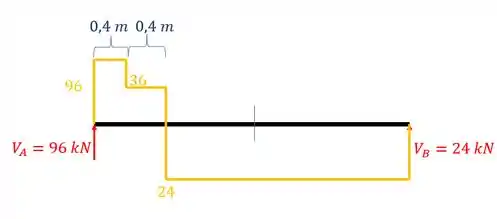
    • Como queremos a maior tensão cisalhante no meio do vão, precisamos do carregamento que ocorre exatamente no meio do vão :

    V = 24   k N

  • Esforço Momento fletor

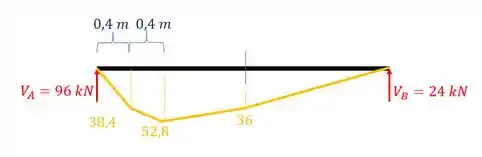
    • Os esforços que age no meio do vão são os esforços que devermos usar, no caso, para o momento fletor, teremos que:

    M = 36   k N m

    Passo 4

    Para as tensões podemos ver o seguinte:

  • As tensões cisalhantes nos pontos a   e   c são zero
  • As tensões normais em b são zero

    • Sabendo isso podemos saber que vamos calcular o seguinte:

    • Tensão cisalhante em b
    • Tensão normal em a   e   c

    Vamos lá então

  • Tensão Máxima cisalhante devido ao cortante em b:

    • V = 24 k N

    Q = 309024,125   m m 3

    I = 70,8   .   10 6   m m 4

    b = 7,4     m m

    τ = V Q I b = 24 k N .     309024,125   [ m m 3 ]     70,8   .   10 6   m m 4   .   7,4   [ m m ] = 0,0142   G P a = 14,2   M P a

  • Tensão Máxima normal no ponto a :

    • M = 36   k N m = 36000   k N m m

    y a = 123,5   m m

    I = 70,8   .   10 6   m m 4

    σ = - M y I = - 36000   k N m m . 123,5 m m 70,8   .   10 6   m m 4 = - 0,0628   G P a

    σ a = - 0,0628   G P a = - 62,8   M P a

  • Tensão Máxima normal no ponto c :

M = 36   k N m = 36000   k N m m

y c = - 123,5   m m

I = 70,8   .   10 6   m m 4

σ = - M y I = - 36000   k N m m . - 123 , 5 m m 70,8   .   10 6   m m 4 = 0,0628   G P a

σ c = 0,0628   G P a = 62,8   M P a

Resposta

τ = 14,2   M P a

σ a = - 62,8   M P a

σ c = 62,8   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine a tensão de cisalhamento máxima na escora se ela for submetida a uma força de cisalhamento V = 20k N
O raio da haste de aço é 30 mm. Se ela for submetida a um cisalhamento V = 25 kN, determine a tensão de cisalhamento máxima.
A escora está sujeita a um cisalhamento vertical V = 130 k N . Construa um gráfico da intensidade da distribuição de tensão de cisalhamento que age na área da seção transversal e calcule a força de ci
Determine a força de cisalhamento máxima V que a escora pode suportar se a tensão de cisalhamento admissível para o material for τ a d m = 40M P a
Faça um gráfico da intensidade da tensão de cisalhamento distribuída na seção transversal da escora se ela for submetida a uma força de cisalhamento V = 15 k N .