Especifique a intensidade de e seus ângulos de direção coordenados , , de modo que a força resultante seja kN.
Passo 1
Falaaa galerinha do RespondeAí, tudo beleza?! Bora lá resolver esse exercício?
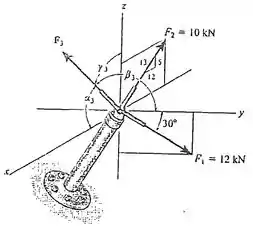
Saca só, o enunciado nos diz que temos forças , e atuando sobre um ponto de um suporte como dado no diagrama seguir:
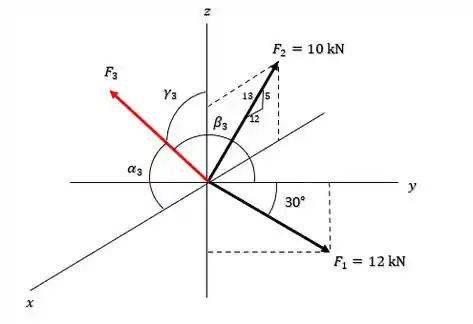
E sabendo que resultante entre essas forças é , ele quer que a gente descubra os ângulos de direção coordenados e a intensidade de . Pra isso vamos precisar decompor as forças em suas componentes de cada eixo pra podermos efetuar os cálculos. Bora lá!
Passo 2
Decompondo através dos seus ângulos de direção, vamos ter que:
Já para a força , ela está contida no plano , de modo que . E o ângulo que faz com o eixo é o mesmo do triangulo retângulo de catetos e , com hipotenusa .
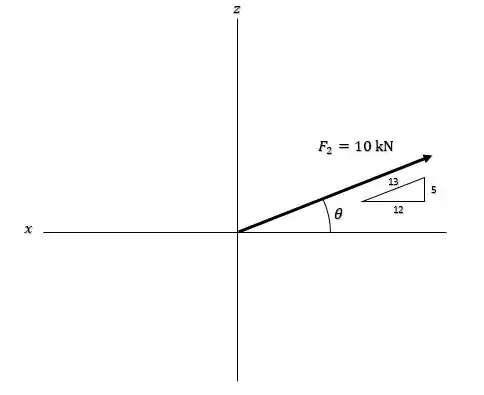
Aqui colocamos o eixo positivo para a esquerda só para não confundir com a primeira imagem, de modo que as componentes da força serão:
Como e , então:
E agora para , ela está contida no plano com um ângulo de com o eixo :
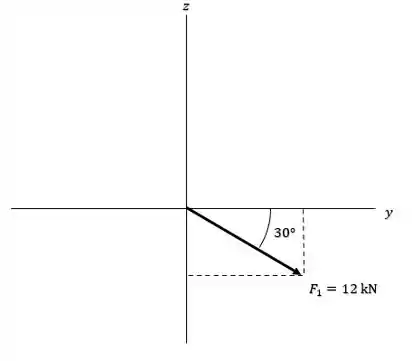
Sendo assim, teremos que suas componentes serão:
Passo 3
Belezera galerinha, agora que sabemos a expressão vetorial das forças, podemos lembrar que a força resultante entre elas possui componente apenas na direção do eixo , ou seja:
Então se a gente somar as componentes do eixo ou do eixo , a soma deve ser igual a . Sendo assim, primeiro para o eixo , temos que:
Isolando , obtemos:
Como , então:
Passo 4
Para o eixo , vamos ter que:
Logo:
Isolando :
Como e , temos que:
Passo 5
Iradoso, agora para o eixo , temos o valor da componente sendo , de modo que:
Logo:
Isolando , veremos que:
Maravilha, agora a gente conseguiu descobrir todas as componentes da força :
Isso quer dizer que sua intensidade será dada como:
Logo:
Passo 6
Show de bolinhas, agora que a gente já tem o valor das componentes e da intensidade, podemos descobrir os ângulos de direção coordenados de , tal que:
Então será:
Para , teremos que:
De modo que será:
E por fim para , vamos obter que:
Portanto:
Prontinha galeura!!
