Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 4.Problemas - Ex. 63
59. O atrito na luva A pode fornecer um momento de resistência máximo de em relação ao eixo x. Determine a maior intensidade da força que pode ser aplicada no braço de modo que ele não gire.
Passo 1
Falaa! Temos ali uma luva, ela sofre uma força , mas há um momento atuando nela que impede que ela rode, o momento de resistência. Queremos descobrir o valor máximo de para que não haja rotação.
Como a luva tem um momento de resistência de , logo a nossa força tem que produzir um momento de no máximo , caso seja maior a luva não irá conseguir resistir mais e o braço irá rodar.
Então temos que achar uma força que produza esse momento. Para isso, vamos usar a análise escalar e conseguir achar o valor da força.
A análise escalar é baseada na fórmula:
Onde e são perpendiculares, e é a menor distância da linha de ação da força até o eixo onde queremos o momento. Chamamos ele de braço de alavanca do momento.
Nessa situação teremos que decompor nossas forças em relação aos eixos coordenados.
A componente da força que é paralela ao eixo x que vai ser no caso a componente x da força, não produz qualquer momento ou tendência para girar em torno desse eixo.
Assim as duas componentes que importam é e .
Vamos definir também o sentido positivo do momento conforme a regra da mão direita.
A distâncias na imagem estão em mm, mas vamos usá-las em m que é a unidade convencional.
Bora lá!
Passo 2
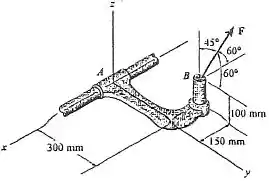
Vamos calcular as componentes da força . No desenho ele nos dá os ângulos que que a força faz com cada eixo coordenado.
Quando ele nos dá a informação assim, a gente multiplica a força pelo cosseno do ângulo que ela faz com o eixo em questão para achar a componente.
Tipo, ela faz com o eixo , então a componente dela no eixo vai ser
E como ela faz com o eixo , a componente é:
Passo 3
Vamos achar os valores de agora. Para a componente , que está “em pé”, a menor distância da linha de ação dela até o eixo é , então a gente diz que:
Já para a componente “deitada”, que é o nosso , a menor distância da sua linha de ação até o eixo é , então
As componentes criam momentos em sentidos opostos. De acordo com a regra da mão direita, o momento de é positivo, porque quando giramos os dedos no sentido da rotação dele, o dedão aponta para a parte positiva de .
Assim nosso momento em relação ao eixo de rotação é:
A primeira componente é negativa pois faz com que o objeto rode no sentido horário em relação ao eixo .
Passo 4
Continuando e substituindo por :
Resposta
A intensidade máxima da força é: