Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 2.Problemas - Ex. 39
O membro delgado de um quarto circular de massa é embutido em seu suporte . Determine o momento de seu peso em relação ao ponto . Use a Tabela D/3 conforme necessário para determinar a localização do centro de massa do corpo.
Passo 1
Olá, joinha?
Esse problema pede que determinemos o momento da força peso em relação ao ponto . Observe a figura:
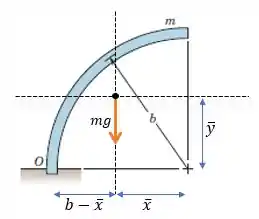
Para calcular o momento, precisamos saber a localização do centro de massa do corpo. O enunciado nos instrui a utilizar a Tabela D/3, mas, na verdade, essa informação encontraremos na Tabela D/4:
Veja que, o raio da nossa figura é , portanto,
E a distância da força peso até o ponto , será .
Passo 2
De posse de tais dados, agora é só calcular o momento em relação ao ponto .
Considerando o sentido horário como positivo:
no sentido horário.