Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 142
Para o estado plano de deformação dado, use o círculo de Mohr para determinar (a) a orientação e a intensidade das deformações principais, (b) a deformação máxima no plano e (c) a deformação de cisalhamento máxima.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, vamos precisar desenhar o círculo de Mohr para as deformações, para fazer isso, precisamos dos pontos X, Y e do centro C do círculo, fazendo isso, conseguimos encontrar a orientação das deformações principais. Para finalizar a letra (a) e encontrar a intensidade das deformações principais, vamos precisar calcular a deformação média e a o raio do círculo de Mohr.
Depois, para as letras (b) e (c), vamos analisar os sinais das deformações principais para encontrar a deformação máxima no plano e a deformação de cisalhamento máxima. Então bora lá!
Passo 2
Então, vamos começar escrevendo as deformações que foram dadas no enunciado:
Agora, com esses valores podemos calcular a deformação média, que será dada por:
Agora, sabemos que os pontos do círculo de Mohr são dados por:
E, agora, vamos calcular o raio do círculo de Mohr, que será dado por:
Com esses valores, podemos finalmente desenhar o círculo de Mohr, que para o nosso caso será:
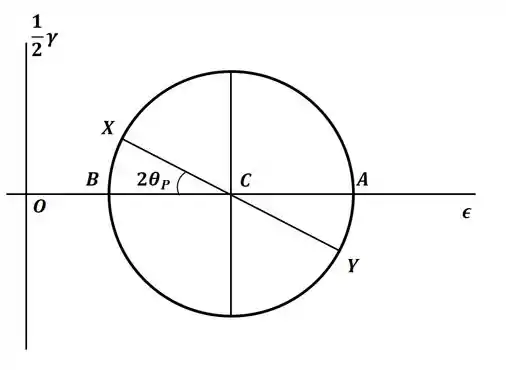
Passo 3
Então, no nosso caso, a direção principal será dada por:
E, substituindo os valores conhecidos, chegamos em:
E, como sabemos que a outra direção principal fica a 90° de inclinação no elemento diferencial (ou seja, a 180° no círculo de Mohr), então a outra direção será:
Agora, para encontrar a intensidade das deformações principais, vamos utilizar as seguintes relações para encontrar as deformações nos pontos A e B do nosso círculo:
Beleza! Fechamos a letra (a).
Passo 4
Agora, para a letra (b), a primeira coisa que devemos notar é que as deformações principais possuem o mesmo sinal, como podemos ver pelo círculo de Mohr também! Ou seja, como sabemos que o círculo tridimensional toca a origem, a nossa deformação normal mínima será:
Sendo assim, a deformação máxima no plano será o próprio diâmetro do círculo de Mohr, ou seja:
Passo 5
Beleza, e agora, para a letra (c), sabemos que a deformação máxima de cisalhamento será dada por:
Então, com os valores encontrados no passo 3 e no passo 4, temos que:
Então, a nossa deformação de cisalhamento máxima será:
Shooow! Fechamos mais um exercício, valeeu!