Enunciado
Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 7.Problemas - Ex. 146
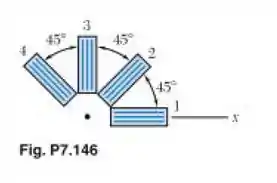
A roseta indicada foi utilizada para determinar as seguintes deformações específicas na superfície de um gancho de guindaste:
(a) Qual deverá ser a leitura do extensômetro 3? (b) Determine as deformações específicas principais e a deformação de cisalhamento máxima no plano das deformações.
Passo 1
Opaa! Fala pessoal, beleza? Bora pra mais um?! Para resolver esse exercício, precisamos notar que os estados 1 e 3 e 2 e 4 estão separados por 90°, sendo assim, conseguimos utilizar a equação para a deformação média nesses intervalos:
Fazendo isso, descobrimos a deformação média, e depois utilizamos a equação novamente, só que com os pontos 1 e 3, para descobrir a deformação 3 pedida na letra (a).
Depois disso, como os pontos 1 e 3 estão nas direções x e y, já temos as deformações nessas direções, feito isso ficará fácil encontrar a deformação de cisalhamento . E com todas as deformações encontradas, conseguimos encontrar o raio do círculo de Mohr, que é o valor que falta para determinar as deformações específicas principais e a deformação de cisalhamento máxima no plano das deformações. Então bora lá!
Passo 2
Tá legal! Vamos começar calculando a deformação média através dos pontos 2 e 4, onde teremos:
Então, utilizando a mesma equação para os pontos 1 e 3, que também estão separados por 90°, teremos:
Isolando e substituindo os valores conhecidos, chegamos em:
Opa! Fechamos a letra (a). Bora pra (b).
Passo 3
Agora, para a letra (b), conforme vimos no passo 1, como as direções 1 e 3 estão alinhadas com os eixos x e y, teremos:
Beleza, com isso, conseguimos encontrar a deformação de cisalhamento, que será dada por:
Substituindo os valores conhecidos, chegamos em:
Com esses valores, agora podemos calcular o raio do círculo de Mohr, que é dado por:
Então, agora podemos calcular as deformações principais pedidas na letra (b), que serão:
Agora, sabendo que a deformação de cisalhamento máxima no plano será o diâmetro do círculo de Mohr, ou seja:
Substituindo os valores conhecidos, teremos:
Shooow! Fechamos mais um exercício, valeeu!