Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 66

Para o estado plano de tensões mostrado, determinar a máxima tensão de cisalhamento, quando: (a) σ x = 100   M P a e σ y = 30 M P a ; (b) σ x = 145   M P a   e σ y = 100   M P a .   (Sugestão: Considerar as tensões de cisalhamento, no plano e fora do plano.)

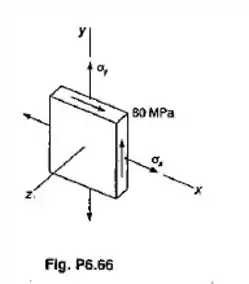
Passo 1

Da letra (a) temos

σ x = 100   M P a

σ y = 30   M P a

τ x y = 80   M P a

Pelo círculo de mohr vamos ter então

σ m e d = 1 2 σ x + σ y = 65   M P a

E para R

R = σ x - σ y 2 2 + τ x y 2 = 35 2 + 80 2 = 87,32   M P a

Podemos então calcular as tensões principais σ a ,   σ b   e   σ c

σ a = σ m e d + R = 65 + 87,32 = 152,32   M P a

σ b = σ m e d - R = - 22,32

σ c = 0

Com isso temos que σ a é o máximo, enquanto σ c é o mínimo

Podemos então calcular o τ m a x

τ m a x = 1 2 σ m a x   - σ m i n = 1 2 σ a   - σ c = 76,16   M P a

Passo 2

Da letra (b) temos

σ x = 145   M P a

σ y = 100   M P a

τ x y = 80   M P a

Pelo círculo de mohr vamos ter então

σ m e d = 1 2 σ x + σ y = 122,5   M P a

E para R

R = σ x - σ y 2 2 + τ x y 2 = 22,5 2 + 80 2 = 8 3,1   M P a

Podemos então calcular as tensões principais σ a ,   σ b   e   σ c

σ a = σ m e d + R = 65 + 87,32 = 205,6   M P a

σ b = σ m e d - R = 39,4

σ c = 0

Com isso temos que σ a é o máximo, enquanto σ c é o mínimo

Podemos então calcular o τ m a x

τ m a x = 1 2 σ m a x   - σ m i n = 1 2 σ a   - σ c = 102,8   M P a

Resposta

a )   τ m a x = 76,16   M P a  

b )   τ m a x = 102,8   M P a  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas peças de madeira de 80x120m m , de seção transversal retangular e uniforme, são unidas por simples colagem das seções chanfradas, como mostrado. Sabendo-se que as máximas tensões admissíveis na j
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado.
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado.
Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado.