Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 5.Problemas - Ex. 138

A viga em balanço mostrada consiste em um perfil em forma de “Z”, de espessura uniforme. Para o carregamento mostrado, determinar a distribuição de tensões de cisalhamento na perna vertical BD. Os eixos x’ e y’ são centroidais e principais da seção transversal.

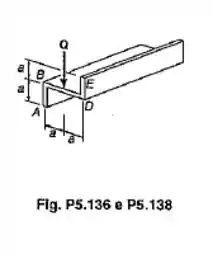
Passo 1

A única coisa que temos desse enunciado é que β = 67,5 ° , já que temos que x ' faz 22,5 ° com o eixo x. 90 - 22,5 = 67,5 .

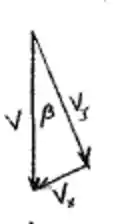
Vamos ter então que

V x = V s e n β

V y = V c o s β

Passo 2

Para a parte DE’ vamos ter então

A = t . a

x - = - a 2

y - = a

Onde " t " representa a espessura uniforme do perfil.

Para a parte E’Y

A = t a - y

x - = 0

y - = 1 2 a + y

Teremos ainda

x ' = x c o s β + y s e n β

y ' = y c o s β - x s e n β

Passo 3

Com isso em mãos podemos começar a calcular as tensões de cisalhamento

Primeiro em relação a V x '

τ 1 = V x ' A D E x - D E ' + A E Y x - E Y ' I y ' t  

τ 1 = V s e n β t a - a 2 c o s β + a s e n β + t a - y 1 2 a + y s e n β 3,08 a 3 t    

τ 1 = V s e n β - t a 2 2 c o s β + t a 2 s e n β + t a - t y a 2 s e n β + y 2 s e n β 3,08 a 3 t

τ 1 = V s e n β - t a 2 2 c o s β + t a 2 s e n β + t a 2 2 s e n β - t a y 2 s e n β + t y a 2 s e n β - t y 2 2 s e n β 3,08 a 3 t

τ 1 = V s e n β - a 2 2 c o s β + a 2 s e n β + a 2 2 s e n β - y 2 2 s e n β 3,08 a 3

τ 1 = V s e n β - a 2 2 c o s β + 3 a 2 2 - y 2 2 s e n β 3,08 a 3

τ 1 = V 0,92 - a 2 2 0,38 + 3 a 2 2 - y 2 2 0,92 3,08 a 3

τ 1 = - V a 2 0,1748 + V a 2 1,2696 - V y 2 0 , 4232 3,08 a 3

τ 1 = V 0,0948 a 2 - 0,4232 y 2 3,08 a 3

Passo 4

Fazemos o mesmo agora, mas em relação a V y '

τ 2 = V y ' A D E y D E ' + A E Y y - E Y ' I x ' t  

τ 2 = V c o s β t a a c o s β + a 2 s e n β + t a - y 1 2 a + y c o s β 0,2521 a 3 t    

τ 2 = V c o s β t a 2 c o s β + t a 2 2 s e n β + t a - t y a 2 c o s β + y 2 c o s β 0,2521 a 3 t

τ 2 = V c o s β t a 2 c o s β + t a 2 2 s e n β + t a 2 2 c o s β - t a y 2 c o s β + t y a 2 c o s β - t y 2 2 c o s β 0,2521 a 3 t

τ 2 = V c o s β a 2 c o s β + a 2 2 s e n β + a 2 2 c o s β - y 2 2 c o s β 0,2521 a 3

τ 2 = V 0,38 a 2 2 ( 0,92 ) + 3 a 2 2 - y 2 2 0,38 0,2521 a 3

τ 2 = V 0,17 4 a 2 + 0,2166 a 2 - y 2 0 , 144 0,2521 a 3

τ 2 = V 0,3906 a 2 - 0,144 y 2 0,2521 a 3

Para finalizar, a tensão total será dada por

τ t = τ 1 + τ 2 = V 0,0948 a 2 - 0,4232 y 2 3,08 a 3 + V 0,3906 a 2 - 0,144 y 2 0,2521 a 3

Resposta

V 0,0948 a 2 - 0,4232 y 2 3,08 a 3 + V 0,3906 a 2 - 0,144 y 2 0,2521 a 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para uma viga extrudada de seção transversal mostrada, determinar:A distribuição das tensões de cisalhamento, causadas por uma força vertical V de 2,5k N aplicada em O .
Para uma viga extrudada de seção transversal mostrada, determinar:A localização do centro de cisalhamento O A distribuição das tensões de cisalhamento, causadas por uma força vertical V de 2,5k N apli
Para uma viga extrudada, com a seção transversal mostrada, determinar:A distribuição de tensões de cisalhamento, causando pela força cortante vertical V, aplicada em O.
Para uma viga extrudada, com a seção transversal mostrada, determinar:A localização do centro de cisalhamento O.
Determinar a localização do centro de cisalhamento O de uma viga de parede fina de espessura uniforme e com a seção transversal mostrada.