Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 6.Problemas - Ex. 8

Para o estado de tensões dado, determinar: (a) os planos principais; (b) as tensões principais.

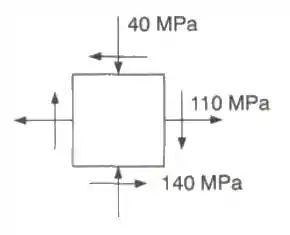
Passo 1

Para resolver essa questão a primeira coias e a mais importante é saber identificar corretamente as tensões normais e cisalhantes, neste caso será o seguinte:

σ x = 100   M P a

σ y = - 40   M P a

τ x y = - 140   M P a

Passo 2

O segundo passo, que já consiste na resolução da letra a , é a determinação dos planos principais onde:

t g 2 θ p = 2 ⋅ τ x y σ x - σ y

Substituindo:

t g 2 θ p = 2 ⋅ - 140 100 - ( - 40 )

t g 2 θ p = - 280 140 = - 2

2 θ p = a r c t g - 2 = - 63,43 °

θ p = - 63,43 2

θ p = - 31,71 °

É necessário colocar o complemente também, então

θ p = - 31,71 ° ; 58,29 °

Passo 3

Agora vamos resolver a letra b , achando as tensões principais que são dadas por:

σ = σ x + σ y 2 ± σ x - σ y 2 2 + τ x y 2

Substituindo:

σ = 100 - 40 2 ± 100 + 40 2 2 + - 140 2

σ = 60 2 ± 24500

σ = 30 ± 156,52   M P a

Ou seja, a tensão máxima vale

σ m á x = 186,52   M P a

E a tensão mínima

σ m í n = - 126,52   M P a

Resposta

a)

θ p = - 31,71 ° ; 58,29 °

b)

σ m á x = 186,52   M P a

σ m í n = - 126,52   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar a localiz
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar a localiz
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar a localiz
Para a viga com o carregamento mostrado, domensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 825k P a .
Para a viga com o carregamento mostrado, dimensionar a seção transversal da viga, sabendo-se que a para o tipo de madeira usada a σ a d m = 12M P a e τ a d m = 860k P a .