Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 82a
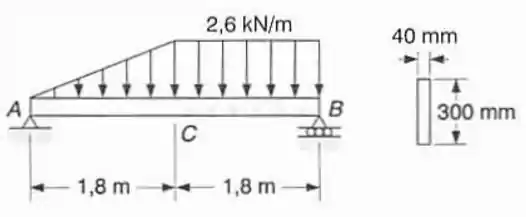
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar a localização e a intensidade o máximo momento fletor na viga e a máxima tensão normal devido à flexão.
Passo 1
Agora a gente vai resolver os problemas com a utilização de funções singulares, mas o que é isso? Olha a função abaixo:
Esse é uma função normal, correto? Mas imagina que eu quero fazer o seguinte: Ignorar o segundo termo quando . Nós podemos fazer escrevendo:
Dessa forma vamos admitir duas hipóteses:
Quando a função fica:
Quando a função fica:
Legal né? É essa propriedade que vamos utilizar neste problema.
Passo 2
Vamos calcular as reações nos pontos e . Para isso vamos fazer o somatório das forças em igual a zero (é um problema de estática, lembre-se). Vamos representar e as componentes das reações em A e a componente da reação em B.
Como só existe uma força em então nem precisamos fazer nenhuma conta .
Já para temos:
Agora a gente tem que ver que terão dois carregamentos distribuídos, uma retangular e outra triangular. Agora a gente precisa trocar esses carregamentos por forças concentradas pontuais . Vamos começar pela retangular que é mais fácil:
Tranquilinho né? Só multiplicar a carga pela distância.
Agora para fazer a triangular a gente vai fazer a mesma coisa mas pegando a média entre e . Porque o carregamento é triangular, ou seja, linear =D
Agora podemos substituir na equação:
Agora vamos calcular o momento no ponto A:
Lembrando que a força pontual equivalente a um carregamento é sempre aplicada no baricentro da sua figura. No caso do retângulo na metade da sua distância e no caso do triângulo 1/3 da base.
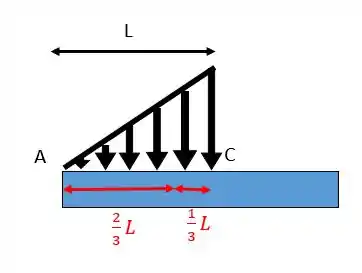
Dessa forma os momentos referentes a cada carregamento distribuído são:
Para o triangular:
Substituindo no momento total aplicado em A:
Logo substituindo na equação anterior:
Passo 3
Agora o importante é achar a função singular que define o carregamento. Vamos relembrar que os carregamentos:
Logo:
Nossa equação mostra que o carregamento começar triangular e depois do ponto aparece um novo carregamento uniforme (retangular). Mas existe um probleminha...
A gente precisa desconsiderar o carregamento triangular depois de . Então vamos adicionar um termo para zera-lo, que é um novo carregamento triangular; mas esse começa com e termina com :
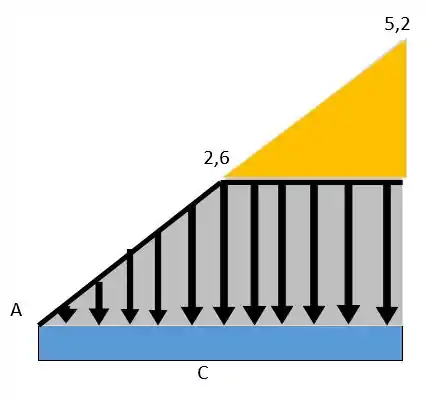
Dessa forma a gente precisa adicionar um carregamento para anular somente a parte amarela que será da forma:
Logo o carregamento total do nosso problema é:
Passo 4
Agora a gente vai integrar essa função em de modo a achar o vetor cortante :
Agora a gente tem que achar a constante , que vai ser igual às forças pontuais aplicadas. No caso temos apenas a reação em A.
Passo 5
Para achar o momento fletor basta que a gente integre novamente =D
A constante é igual a qualquer momento puro que não existe em nenhum ponto logo:
Resposta
a)