Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 82b

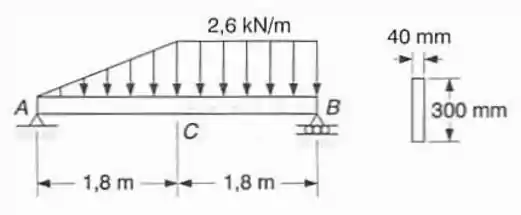
Pede-se: (a) Para a viga com o carregamento mostrado e usando funções singulares, escrever as equações que definem as curvas do diagrama de força cortante e de momento fletor; (b) determinar a localização e a intensidade o máximo momento fletor na viga e a máxima tensão normal devido à flexão.

Passo 1

Para fazer a letra B a gente vai precisar das nossas equações da força cortante e momento fletor calculados na letra A. Eles são:

V x = - 2,6 3,6 x 2 - 2,6 × x - 1,8 1 + 5,2 3,6 x - 1,8 2 + 2,73

M x = - 2,6 1,2 x 3 - 1,3 × x - 1,8 2 + 5,2 1,2 x - 1,8 3 + 2,73 x

Passo 2

Agora para achar o maior momento fletor a gente tem que igualar a força cortante a zero (porque a cortante é a derivada do momento fletor, por isso, quando igual a zero, representa seu máximo).

V x = - 2,6 3,6 x 2 - 2,6 × x - 1,8 1 + 5,2 3,6 x - 1,8 2 + 2,73

A gente vai ter que pensar em duas situações, para x < 1,8 :

V x = - 2,6 3,6 x 2 + 2,73 = 0

x = 1,944   m

Um absurdo!!! Que blasfémia!!! x não pode ser menor que 1,8 e igual a 1,944 ao mesmo tempo não é mesmo? Então resta a segunda opção:

Pegando 1,8 ≤ x :

V x = - 2,6 3,6 x 2 - 2,6 × x - 1,8 + 5,2 3,6 x - 1,8 2 + 2,73 = 0

0,722 . x 2 - 7,8 . x + 12,09 = 0

Agora a gente tem que utilizar bháskara...

Passo 3

x = 7,8 ± 7,8 2 - 4 ( 0,722 ) ( 12,09 ) 2 . 0,722

x = 7,8 ± 25,924 1,444

x = 7,8 ± 5,092 1,444

x = 7,8 + 5,092 1,444 = 8,9   m

Esse valor é inválido porque está fora da barra, logo:

x = 7,8 - 5,092 1,444 = 1,875   m

Já achamos o ponto x = 1 , 875 !

Passo 4

Agora vamos achar o valor do máximo momento fletor:

M x = - 2,6 1,2 x 3 - 1,3 × x - 1,8 2 + 5,2 1,2 x - 1,8 3 + 2,73 x

M m á x = - 2,6 1,2 1,875 3 - 1,3 × ( 1,875 - 1,8 ) 2 + 5,2 1,2 ( 1,875 - 1,8 ) 3 + 2,73 ( 1,875 )

M m á x = - 14,28 - 0,007 + 0,002 + 5,12

M m á x = - 9,16   k N ⋅ m

Passo 5

Agora a gente tem que achar a máxima tensão normal devido à flexão, que é dada pela equação:

σ = M c I

Onde M é o momento fletor, c a distância da linha neutra até o ponto que estamos calculando (como queremos o valor máximo será sempre na superfície) e I o momento de inércia, dado na tabela do livro.

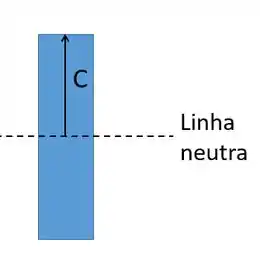
O momento fletor a gente já calculou e vale - 9,16   k N . O nosso perfil pode ser achado pela fórmula:

I = 1 12 b h 3

I = 1 12 . 0,040.0,300 3 = 9 × 10 - 5   m 4

Como a altura da viga é de 300   m m vamos ter que:

c = D 2 = 300 2 = 150   m m

Agora podemos calcular a máxima tensão normal:

σ = M c I

σ = - 9,16 × 10 3 × ( 150 × 10 - 3 ) 9 × 10 - 5

σ = 15,26   M P a

Resposta

b)

x = 1,875

M m á x = - 9,16   k N ⋅ m

σ = 15,26   M P a

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Desenhar os diagramas de força cortante e de momento fletor para a viga com o carregamento mostrado.
Determine as equações das curvas dos diagramas da força cortante e do momento fletor, para a viga com carregamento indicado. (Adotar a origem no ponto A.)
Determine as equações das curvas dos diagramas da força cortante e do momento fletor, para a viga com carregamento indicado. (Adotar a origem no ponto A.)
Determine as equações das curvas dos diagramas da força cortante e do momento fletor, para a viga com carregamento indicado. (Adotar a origem no ponto A.)
Determine as equações das curvas dos diagramas da força cortante e do momento fletor, para a viga com carregamento indicado. (Adotar a origem no ponto A.)