Enunciado
Mecânica e Resistência dos Materiais - Hibbeler - Estática- Ed: 14º - Capítulo 8.Problemas - Ex. 67
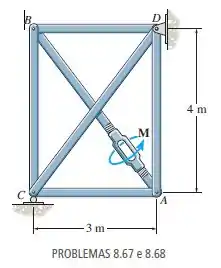
Um esticador, semelhante ao mostrado na , é usado para tracionar o elemento AB
da treliça. O coeficiente de atrito estático entre os parafusos com rosca quadrada e o esticador é . Os parafusos possuem raio médio de e avanço de rosca de . Se um torque de for aplicado ao esticador, para aproximar os parafusos, determine a força em cada elemento da treliça. Nenhuma força externa atua sobre a treliça.
Passo 1
Oi tudo bem? Vamos resolver este exercício.
Sabemos que o ângulo de fricção é dado por:
Portanto:
O ângulo de avanço do parafuso é dado por:
Substituindo os dados, temos que:
Passo 2
Agora vamos calcular o menor torque necessário para afrouxar o parafuso. Temos que:
Logo:
Resposta
Exercícios de Livros Relacionados
O macaco mostrado foi projetado para levantar carros de carroceria pequena. O parafuso é rosqueado no colar articulado em B e o eixo gira em um rolamento de esferas em A. A rosca tem um diâmetro médio
Para ambas as condições (a) e (b), conforme declarado no Prob. 6/66, determine a magnitude e a direção da força P necessária para começar a abaixar o corpo de 100 lb.
A posição vertical do bloco de 100 kg é ajustada pela cunha ativada por parafuso. Calcule o momento M que deve ser aplicado ao cabo do parafuso para levantar o bloco. O parafuso de rosca única possui
Um disco uniforme de raio r = 250 mm é fixado em A a uma haste AB de 650 mm de massa desprezível que pode girar livremente em um plano vertical em torno de B. se a haste for deslocada 2 ° da posição m
As duas cunhas mostradas são usadas para ajustar a posição da coluna sob uma carga vertical de 5 kN. Determine a magnitude das forças P necessárias para levantar a coluna se o coeficiente de atrito pa