Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 6.Problemas - Ex. 73
O macaco mostrado foi projetado para levantar carros de carroceria pequena. O parafuso é rosqueado no colar articulado em B e o eixo gira em um rolamento de esferas em A. A rosca tem um diâmetro médio de 10 mm e um avanço (avanço por rotação) de 2 mm. O coeficiente de atrito das roscas é de 0,20. Determine a força P normal para a alça em D necessária
(a) para elevar uma massa de 500 kg da posição mostrada e (b) para baixar a carga da mesma posição. Despreze o atrito no pivô e no rolamento em A.
Passo 1
Primeiro, vamos isolar e desenhar o diagrama de corpo livre do membro AC, a fim de determinar a força axial no parafuso
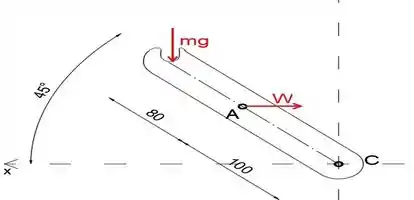
Equacionando a soma dos momentos sobre o ponto C a zero, determinaremos a força W
Passo 2
(a) equação do momento de equilíbrio do parafuso é
(1)
Em que W a força axial
O r é raio
α é o ângulo que o fio faz com o eixo y, uma vez que se move 2 "" mm por revolução, e a circunferência de um círculo é 2rπ, podemos determinar α
Determinaremos o ângulo uma vez que conhecemos a força de fricção
Finalmente, colocando todos os valores conhecidos na equação (1), vamos determinar M
Uma vez que o comprimento do braço é 150 "" mm, a força P aplicada a D necessária para produzir este momento é
Passo 3
(b) Observe que ao tentar afrouxar o dispositivo, a força de atrito terá direção oposta, portanto o ângulo que R resultante faz com o eixo x é (ϕ-α), portanto a equação de equilíbrio de momento é
(2)
Como os parâmetros W, r, ϕ e α são iguais aos da equação (1), colocando todos os valores conhecidos na equação (2), determinaremos M’
Uma vez que o comprimento do braço é 150 "" mm, a força P aplicada a D necessária para produzir este momento é