Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 11.Problemas - Ex. 38
Para a estrutura do Prob. 11.37, determinar:(a) a distância h para que o coeficiente de segurança em relação á flambagem seja máximo;(b) o correspondente coeficiente de segurança para m=7500kg.
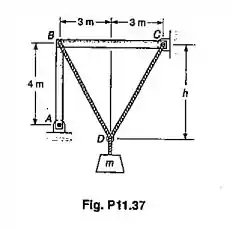
Passo 1
Fala aí, pediu outra questão de flambagem com coeficiente de segurança?
Vamos primeiro trazer alguns dados que a questão anterior nos dá e que precisaremos ter aqui:
Aqui a gente precisa encontrar a altura que maximiza o coeficiente de segurança, lembrando que:
Lembrando que pro peso crítico é dado por:
Precisamos minimizar o peso admissível nas barras nesse caso, então bora desenhar o nosso diagrama de corpo livre e começaremos pelo cabo:
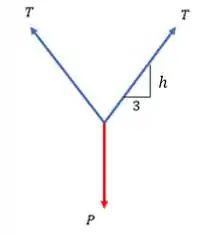
Desenhando o DCL dos cabos a gente pode relacionar o esforço de tração nos cabos T, com o peso P do bloco e depois disso poderemos relacionar com o peso admissível de cada coluna e a gente pode ver no DCL como isso vai ficar:
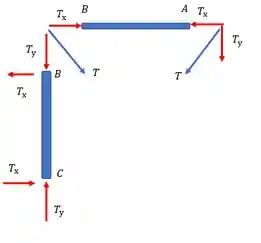
Após encontrar o ótimo, vamos substituir na fórmula para o menor dos pesos críticos encontrados e encontrar o fator de segurança.
Passo 2
Vamos as relações que a gente precisa, a primeira é no cabo. Se a gente olhar o triângulo na figura vai ficar bem fácil a decomposição. Vamos fazer o somatório dos esforços no cabo para achar uma relação de P.
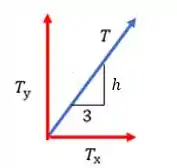
Assim o somatório das forças fica para os dois cabos:
A gente tira então que:
E será o peso que vai causar flambagem na barra vertical, e um jeito beeem fácil de acharmos a relação de com o peso é através do próprio da figura a gente pode tirar a seguinte relação:
Então:
Passo 3
Vamos avaliar que comprime a barra AB, portanto vamos apenas avaliar a flambagem para esta barra, então a relação precisa ser verdade.
Que no caso faz a barra AB resistir a flambagem com segurança e lembrando que:
O momento de inércia já foi calculado antes e vale:
Substituindo os valores, temos.
E substituindo na fórmula para :
E como:
Temos:
Rearrumando a gente tem:
Passo 4
De boa né não está relacionado á , e se ele é constante podemos otimizar a altura para que os coeficientes de segurança sejam iguais.
Que no caso faz a barra AB resistir á flambagem com segurança e lembrando que:
E para esse tipo de barra o momento de inércia é:
Substituindo os valores, temos.
E substituindo na fórmula para :
E como:
E aí comparando temos:
Então:
Enfim comparando os dois fatores encontraremos o .
E aí:
Passo 5
Pro item b. vamos resolver rapidinho essa parada. Nesse exercício a gente já sabe que o fator de segurança vai ser o mesmo independente de por onde a gente o encontre, sendo assim pegaremos o mais fácil:
Lembrando que:
Temos: