Uma coluna de comprimento efetivo igual a 4,8m será fabricada soldando-se juntos dois perfils laminados de aço C150x15,6. Usando-se E=200GPa, determinar a carga centrada admissível, se um coeficiente de segurança de 2,8 é desejado.

Passo 1
Fala aí, pediu outra questão de peso crítico?
Temos aqui uma seção composta aqui e precisamos calcular peso crítico para encontrar o peso admissível já que a fórmula nos dá.
Lembrando que pro peso crítico é dado por:
E aqui vamos atrás desse momento de inércia que vai ser fundamental pro cálculo do peso crítico, bora lá?
Passo 2
Sobre esse momento de inércia é o seguinte, esse tipo de perfil C não é exatamente retangular nas bordas portanto calcular na mão nos traria apenas um valor aproximado e não o real. O Jeito correto de se fazer é procurar no final do livro a tabela para o tipo de perfil e de lá retirar as dimensões como faremos.
A tabela utilizada foi a de perfis C desiguais e encontramos para o perfil C150x15,6.
Temos a área:
A largura da mesa:
E a distância da aba até o centro da peça:
E os momentos de inércia de cada eixo:
Agora vamos analisar a disposição das peças na figura para avaliar como calcular o momento de inércia do sistema:
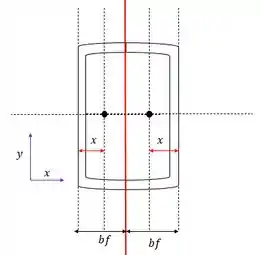
E aqui vemos o seguinte, não há nenhum eixo paralelo ao x então dispensa o uso do teorema dos eixos paralelos, já para y temos dois que estão distantes do centro do sistema então mãos á obra.
E para y usaremos o teorema dos eixos paralelos.
E substituindo os valores temos:
Então y é o nosso eixo fraco pois possui menor momento de inércia.
Passo 3
Vamos enfim para o nosso querido peso crítico:
Substituindo os valores, temos.
E aí, como usamos as dimensões em gigapascal e milímetros o resultado sai direto em kilonewtons:
E enfim calculamos o fator de segurança: