Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 69

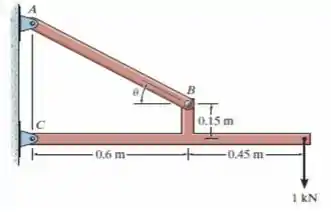
A estrutura está sujeita a carga de 1   k N . Determine a tensão de cisalhamento média no parafuso em A em função do ângulo da barra θ . Represente essa função em gráfico para 0 ≤ θ ≤ 90 ° e indique os valores de e para os quais essa tensão é mínima. O parafuso tem diâmetro de   6   m m   e está sujeito a cisalhamento simples.

Passo 1

Antes de calcularmos as reações nos suportes, vamos fazer um diagrama com as forças que estão atuando nesse problema a fim de facilitar a visualização. Assim, teremos

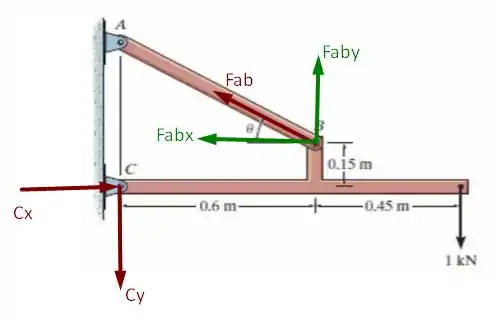
Onde o vetor F a b foi decomposto em 2 componentes: um vertical e um horizontal, traçados em verde no diagrama e podem ser interpretadas como

F a b x = F a b ⋅ cos ⁡ θ   e   F a b y = F a b ⋅ s e n ( θ )

Passo 2

Como queremos encontrar a tensão de cisalhamento média em função do ângulo θ vamos fazer as reações no suporte para encontrarmos a força que precisamos para o cálculo da tensão que é F a b , assim, temos

∑ M c = 0

Adotando o sentido anti-horário como positivo vamos ter

F a b x ⋅ 0.15 m + F a b y ⋅ 0.6 m - 1 k N ⋅ 1,05 m = 0

F a b ⋅ cos ⁡ θ ⋅ 0.15 m + F a b ⋅ s e n ( θ ) ⋅ 0.6 m - 1 k N ⋅ 1,05 m = 0

F a b ⋅ cos ⁡ θ ⋅ 0.15 m + F a b ⋅ s e n θ ⋅ 0.6 m = 1 k N ⋅ 1,05 m

F a b ⋅ cos ⁡ θ ⋅ 0.15 m + s e n θ ⋅ 0.6 m = 1 k N ⋅ 1,05 m

F a b = 1 k N ⋅ 1,05 m cos ⁡ θ ⋅ 0.15 m + s e n θ ⋅ 0.6 m

Passo 3

Lembrando que tensão de cisalhamento é dado por

τ = F a b A p a r a f u s o

Onde

A p a r a f u s o = π ⋅ d i â m e t r o 2 4

Assim, temos

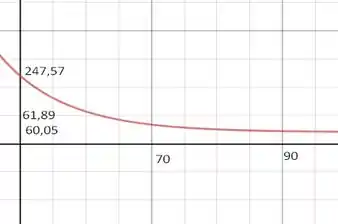
τ = 1 k N ⋅ 1,05 cos ⁡ θ ⋅ 0.15 + s e n θ ⋅ 0.6 ⋅ 4 π ⋅ d i â m e t r o 2

Para encontrarmos o valor de τ em função do ângulo, esse ângulo vai ser um dos nossos pontos críticos, então, vamos derivar nossa função em relação a θ e igualar a 0.

d τ d θ =   4,2 k N π ⋅ d i â m e t r o 2 ⋅ [ sin ⁡ θ ⋅ 0.15 - c o s θ ⋅ 0.6 cos ⁡ θ ⋅ 0.15 + s e n θ ⋅ 0.6 2 ]

Como não podemos ter o denominador igual a 0, para que tenhamos d τ d θ = 0 precisamos ter

( sin ⁡ θ ⋅ 0.15 - c o s θ ⋅ 0.6 ) ⋅ 4,2 k N = 0 →   sin ⁡ θ ⋅ 0.15 - c o s θ ⋅ 0.6 = 0

sin ⁡ θ ⋅ 0.15 = c o s θ ⋅ 0.6 → t g θ = 0.6 0.15 → t g θ = 4

θ = A r c t a n 4 → θ = 75,96 °

Representando essa função em um gráfico genérico vamos ter

Resposta

θ = 75,96 °

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Duas pranchas de madeira, cada uma com 12 mm de espessura e 225 mm de largura são unidas pela junta de encaixe mostrada na figura. Sabendo que a madeira utilizada rompe por cisalhamento ao longo das f
A força axial na coluna que suporta a viga de madeira mostrada é P= 75KN. Determine o menor comprimento L admissível para chapa de contato para que a tensão de contato na madeira não exceda 3 MPa.
Quando a força P alcançou 8 KN, o corpo de prova de madeira mostrado na figura falhou sob cisalhamento ao longo da superfície indicada pela linha tracejada. Determine a tensão de cisalhamento média ao
Determine o diâmetro do maior orifício circular que pode ser feito em uma tira de poliestireno com espessura de 6 mm, sabendo que a força exercida pela punção é de 45 kN e que a tensão de cisalhamento
Uma carga P é aplicada a uma barra de aço suportada por uma chapa de alumínio na qual foi feito um furo de 12 mm conforme mostra a figura. Sabendo que a tensão de cisalhamento não deve exceder 180 MPa