Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 1.Problemas - Ex. 64
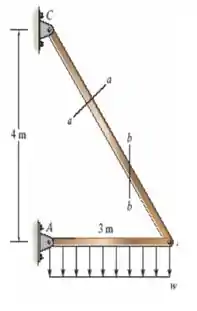
A estrutura de dois elementos está sujeita a um carregamento distribuído mostrado. Determine a tensão normal média e a tensão de cisalhamento média que agem nas seções e . A seção transversal quadrada do elemento tem . Considere .
Passo 1
E aí meus consagrados como vocês estão? Prontos para mais uma questão maneira?
Vamos lá, antes de tudo vamos deixar aqui nossos dados que foram fornecidos pelo enunciado de acordo com a notação que usaremos, assim, temos
Como temos um triângulo retângulo é natural pensarmos no teorema de Pitágoras e é exatamente isso que vamos utilizar assim vamos ter
Para facilitar nosso problema na hora de fazer um diagrama de corpo de livre vamos concentrar nossa carga distribuída no centro da barra de e seu módulo valerá
Feitas essas considerações vamos lembrar como se calcula a tensão normal média e a tensão de cisalhamento média, basta seguir as seguintes fórmulas:
Com
P: resultante da força normal;
A: Área da seção transversal;
F: Força cortante total;
Área cortante;
Passo 2
Agora é a hora de botar a mão na massa, meus amigos. Bora lá, vamos chamar a barra horizontal de e teremos, para essa parte da estrutura, o seguinte diagrama de forças:
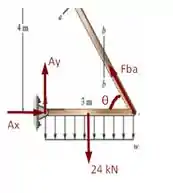
Devemos reparar que a força pode ser decomposta em uma componente horizontal e uma componente vertical em função de senos e cossenos onde teremos:
Pois bem, agora vamos utilizar as equações de equilíbrio para esse problema, ou seja, o somatório das forças em uma determinada direção será igual a zero. Para o membro teremos (adotando o sentido anti-horário como positivo para o momento):
O valor de no nosso problema vai ser igual o valor de , assim, nós conseguimos descobrir o valor de fazendo
Pois bem, para a seção já estamos aptos a encontrarmos as tensões normais que serão dadas pelo quociente (divisão) da força normal pela área, então, encontraremos com isso o seguinte
Lembrando que podemos fazer a conversão para a unidade mais usual obtendo
Já para a tensão de cisalhamento pra seção ela é nula por conta da forma como a inclinação estará então teremos .
Passo 3
Vamos lá meu pequeno gafanhoto, não desista, você já chegou até aqui! Para finalizar nosso problema resta-nos, agora, calcular as mesmas tensões calculadas anteriormente só que agora para a seção , para isso vamos utilizar a componente horizontal da nossa força dada por
Agora o passo final pra concluirmos esse problema só substituindo dados é calcular a área da seção . Para esse caso, a área não é completamente retinha, então, como ela apresenta uma inclinação, sua área será dada por
Dessa forma, agora é só partir pro abraço e substituir valores nas fórmulas das tensões de tal forma que obteremos:
Acabamos mais uma, até que foi de boas, né?
