Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 7.Problemas - Ex. 137
Expressar o comprimento de uma tira de madeira compensada do Exemplo 7.7, em termos de e , considerando que a viga deve ser de igual resistência, quando estiver suportando um carregamento uniformemente distribuído.
Passo 1
Fala aí, galerinha!! Para resolver esse problema a gente vai ter que achar uma o nosso como uma função de . Para isso a gente vai ter que utilizar principalmente aquela nossa equação da tensão admissível.
Então a gente tem que basicamente achar o momento fletor dessa viga e o módulo de resistência dela.
vamos fazer isso para duas situações, um ponto qualquer e um ponto específico daí é só comparar os dois resultados, então partiu?
Pessoal!! Só prestem bem atenção porque o carregamento é distribuído hein!!!
Passo 2
Primeiro vamos observar a seção desta viga, que é retangular:
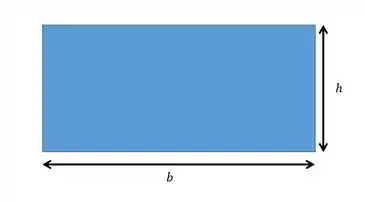
Tranquilo né? Mas mesmo sendo tranquilo é muito importante entender que a seção sempre será um retângulo, a única coisa que vai mudar é a altura.
Então vamos calcular o módulo resistente da seção , que é dado pelo momento de inércia dividido pela maior distância que se pode achar entre a linha neutra e a superfície.
Como temos um retângulo o momento de inércia é dado por:
e, como a linha neutra se localiza no centro do retângulo, a distância é igual a:
Substituindo no módulo resistente:
Show de bola!
Passo 3
Agora vamos calcular o momento fletor máximo que esta viga suporta. Como o problema nos forneceu uma equação para o carregamento vamos utilizar esssa equação para achar o momento fletor.
Se a distribuição é uniforme então:
Mas como a gente faz isso? Basta integrar duas vezes da primeira a gente encontra a força cortante e da segundo o momento fletor:
Esse sinal negativo é da fórmula hein! Não pode esquecer!
Resolvendo a integral ficamos com:
Agora é só integrar novamente e vamos achar o momento fletor:
Repare que agora não existe o sinal negativo!
Passo 4
Estamos quase no fim! UHULLLLL
Agora chegamos no ponto mais importante desta questão que é aplicar o momento fletor em conjunto com o nosso módulo resistente e comparar com a tensão admissível da seguinte forma:
Lembrando que:
e
obs: Precisamos apenas do módulo =D
Vamos substituir os valores que calculamos:
Simplificando:
Essa valor que achamos é para qualquer ponto da nossa viga, logo, deve valer também para , porque ? Porque é onde o momento fletor máximo se localiza! Assim, ficará da seguinte forma:
Substituindo em..
Vamos obter:
Simplificando:
Passo 5
Viram que temos duas equações com ? Então agora é só igualar as duas:
E
Igualando:
Simplificando:
Nós podemos expressar o comprimento como:
Substituindo :