Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 92
Uma extensão de estabilizador para um guindaste móvel é projetada para carregar navios. A viga tem uma massa de com centro de massa em seu comprimento médio. A lança tem uma massa de com centro de massa a da extremidade . A carruagem de é simétrica em relação à sua linha de carga. Calcule a magnitude da força suportada pela dobradiça em para uma carga .
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar o módulo da força que a dobradiça em suporta devido a carga , a carruagem de , a viga de e a lança de .
Então bora resolver! Esse problema é bem simples, vamos começar analisando a viga .
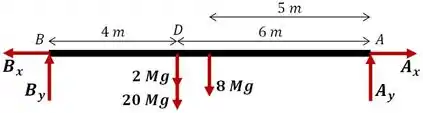
Como a estrutura como um todo está em equilíbrio, a viga também deve estar. Podemos então usar o somatório de momentos em torno de para descobrir a reação , já que o momento em torno desse ponto elimina três das nossas incógnitas dos cálculos: , e . Logo:
Passo 2
Suave né? Ainda pela condição de equilíbrio, vamos usar o somatório das forças atuantes na viga nas direções e :
Passo 3
Show! Agora vamos pegar a outra componente da estrutura, a lança .
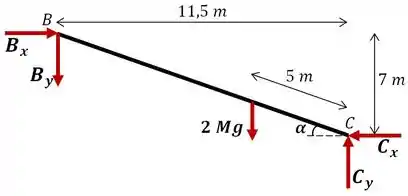
Onde é dado por:
No passo anterior nós já encontramos a componente da força suportada pela dobradiça e sabemos também que . Logo, se descobrirmos resolvemos nosso problema.
Pela mesma condição de equilíbrio da estrutura, podemos fazer o somatório de momentos em torno de , assim eliminamos as outras incógnitas que não são foco do problema e, com isso, determinamos . Então:
Passo 4
Tranquilo né? Agora ficou fácil determinar a magnitude da força suportada pela dobradiça em , ela é dada por:
É só isso, galera! Bem de boa né?!
Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 