Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 100
Calcule a força no elo das pinças de elevação que se cruzam sem se tocar.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a força na barra de ligação das pinças que carregam um peso de .
Então bora resolver! Esse problema é bem simples, uma vez que as pinças são simétricas, podemos analisar a pinça que os resultados são os mesmos para a pinça . Vamos começar então pelo diagrama de corpo livre da pinça :
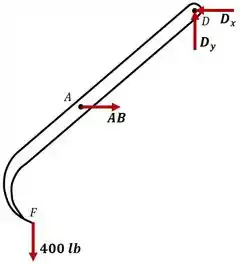
Antes de começarmos é importante lembrar que as pinças dividem o peso da carga igualmente. Logo, o peso suportado pela pinça em é:
Passo 2
Como a estrutura como um todo está em equilíbrio, a pinça também deve estar. Podemos então usar o somatório de forças na direção vertical para determinar .
Além disso, pela geometria da barra temos que:
Passo 3
Até aqui tudo certo! Ainda pela condição de equilíbrio, vamos usar o somatório de momentos em torno de para determinar a tensão :
É só isso, galera! Bem de boa né?!
Partiu pra próxima!
HYPERLINK "https://emojiterra.com/pt/rosto-piscando/" 