Enunciado
Mecânica e Resistência dos Materiais - J. L. Meriam - Estática - Mecânica para Engenharia- Ed: 7º - Capítulo 4.Problemas - Ex. 94
A figura ilustra um problema comum associado a estruturas simples. Sob os carregamentos , as vigas podem girar, a viga de cumeeira em pode baixar e as paredes e podem girar para fora, conforme mostrado na parte da figura. Esse fenômeno às vezes é claramente observado em antigas estruturas de fazendas de madeira como uma curvatura central da viga do cume quando vista de lado. Uma solução simples é mostrada na parte da figura. Uma corrente ou cabo é esticado entre os fixadores em e , e o esticador é apertado até que uma tensão adequada seja alcançada, evitando assim a inclinação das paredes para fora. Para determinados valores da dimensão e das cargas pontuais (que resultam das cargas distribuídas da viga e dos pesos da cobertura e quaisquer cargas adicionais, como neve), calcule a tensão necessária para que não haja forças externas nas paredes em e . Suponha que o suporte das vigas na viga do cume seja puramente horizontal e que todas as juntas estejam livres para girar.
Passo 1
Fala galera, tudo certo? Bora fazer mais um exercício? Prometo que vai ser bem rapidinho!
O enunciado nos pede para determinar a tensão necessária para que não haja forças externas nas paredes em e .
Então bora resolver! Apesar do enunciado grande, podemos encontrar essa tensão de uma forma bem simples. Vamos começar analisando a parte do telhado separadamente, como ele é simétrico, os resultados valem para o lado . Fazendo o diagrama de corpo livre temos:
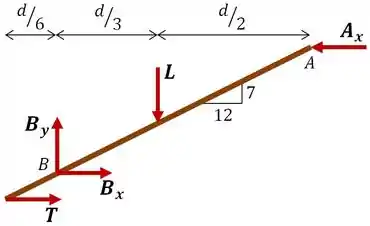
Vamos assumir a hipótese de que as reações na direção são nulas, já que não há forças aplicadas nessa direção, logo:
Passo 2
Show! Como a estrutura está em equilíbrio, podemos fazer o somatório de forças em torno de , o que elimina a necessidade de determinar , para encontrar a tensão .
Ufa! Essa já foi hein? Partiu pra próxima!
