Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.3 - Ex. 23
Faça referência ao enunciado e à figura do Prob. 2/22. Quando o pino está na posição , determine os componentes e da força que a mola de módulo exerce sobre o pino.
Prob. 2/22: O comprimento original da mola de módulo é . Determine os componentes e da força que a mola exerce no pino , quando ele está na posição . (A força em uma mola é dada por , onde é o alongamento da mola em relação ao seu comprimento original.)
Passo 1
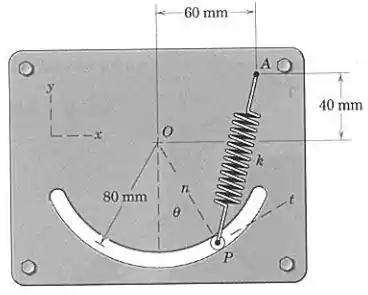
Pessoal, primeiro vamos determinar o comprimento final da mola, a fim de calcular a deformação mais tarde, beleza? Pela figura, vemos que as coordenadas do ponto em relação à origem são e as do ponto são , tudo em milímetros.
Então, quando , temos:
Passo 2
Agora vamos calcular o módulo da força na mola:
onde e é a diferença entre o comprimento final e o comprimento original da mola, em metros:
Passo 3
Sendo o ângulo entre a mola e a horizontal, temos:
Então, o ângulo entre a mola e o eixo da figura (tangente ao círculo) será:
Logo,