Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.3 - Ex. 28
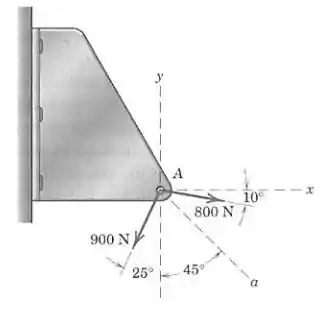
A placa de união está submetida às duas forças mostradas. Substitua-as por duas forças equivalentes, na direção e na direção . Determine os módulos de e . Resolva geometricamente e graficamente.
Passo 1
No desenho a seguir, representamos as forças originais em preto, a resultante em azul e as forças equivalentes e em vermelho:
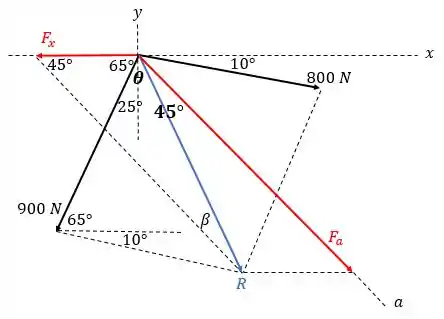
Usando a lei dos cossenos, podemos calcular o módulo :
Passo 2
Para calcular o ângulo entre a força de e a resultante , usamos a lei dos senos:
Agora, note que:
Passo 3
Finalmente, podemos calcular os módulos e por meio da lei dos senos:
Analogamente,
Resposta
Exercícios de Livros Relacionados
Expresse F 1 , F 2 e F 3 como vetores cartesianos.
Determine a intensidade da força resultante que atua sobre a argola e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Determine a intensidade da força resultante e sua direção, medida no sentido anti-horário a partir do eixo x positivo.
Expresse F 1 , F 2 e F 3 como vetores cartesianos.