Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 12.Problemas - Ex. 31

O feixe de molas à mesma tensão de flexão máxima em todo seu comprimento. Se a espessura das chapas de cada lâmina for t e se uma puder deslizar livremente entre a outra, mostre que o feixe de molas deve ter a forma de um arco de círculo para que a mola inteira fique achatada quando for aplicada uma carga P suficientemente grande. Qual é a tensão normal máxima no feixe de molas? Considere que ele foi construído com n tiras cortadas de uma chapa em forma de losango com espessura t e largura b . O módulo de elasticidade para o material é E . Dica: Mostre que o raio de curvatura do feixe de molas é constante.

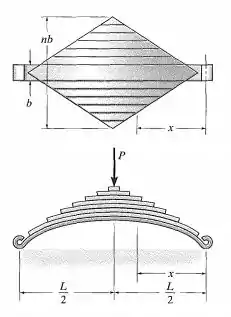
Passo 1

Primeiro, vamos fazer o DLC:

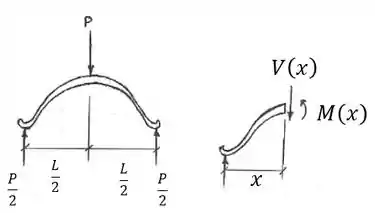
Sendo assim, temos:

I x = 1 12 2 n L x b t 3 = n b t 3 6 L x  

Passo 2

Sendo assim, temos que a tensão máxima σ m á x :

σ m á x = M x c I x σ m á x = P 2 x t 2 n b t 3 6 L x σ m á x = 3 P L 2 n b t 2

Passo 3

Por fim, temos:

1 ρ = M x E I x = P 2 x E n b t 3 6 L x = 3 P L n b t 3 = c t e

Resposta

σ m á x = 3 P L 2 n b t 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Para a viga com o carregamento mostrado, determinar:A declividade no ponto A
Para a viga prismática com o carregamento mostrado, determinar:A deflexão no ponto E
Para a viga com o carregamento mostrado, determinar:A declividade no ponto A
Para a viga prismática com o carregamento mostrado, determinar:A declividade no ponto A
Para a viga com o carregamento mostrado, determinar:A declividade no ponto D