Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Beer - Mecânica dos Materiais- Ed: 7º - Capítulo 4.Problemas - Ex. 37

Vigas de madeira e chapas de aço são aparafusadas firmemente para formar o elemento composto mostrado na figura. Usando os dados da tabela abaixo, determine o maior momento fletor admissível quando a viga é flexionada em torno do eixo horizontal.

Passo 1

Quando temos mais de um material na nossa barra precisamos converter um deles para facilitar o nosso cálculo.

Sabemos que o nosso fator a ser calculado é dado por:

n = E p a r t e   t r a n s f o r m a d a   E p a r t e   i n t a c t a  

Vamos transformar então a madeira em uma correspondente em aço.

n = E m a d e i r a   E a ç o   = 2 × 10 6 29 × 10 6 = 0,069

E para mudarmos a largura do alumínio precisamos fazer a seguinte conta.

b ' = n b = 0 , 069   .   6 = 0,414   i n

Sendo assim a nova seção é dada por:

Nosso objetivo é determinar os momentos fletores, e a fórmula que relaciona a tensão com o momento é dado por:

σ x = - M y I

E se verificarmos a estrutura que foi transformada, teremos que usar a seguinte equação:

σ x = - n M y I

Agora já podemos determinar o momento de inércia.

Passo 2

Agora que temos a LN, podemos determinar o momento de inércia, e o momento de inércia vai ser dado pela seguinte equação:

I = I 1 + I 2 + I 3 + ( A 1 d 1 2 + A 3 d 3 2 )

Em que as áreas já definimos no passo anterior, e os valores de I 1   , I 2   e   I 3 são os momentos de inércia de cada uma das seções mais simples. E d 1   e   d 3 são as distâncias do centroide de cada uma das peças mais simples até a LN, assim as medidas da nossa seção são dadas abaixo.

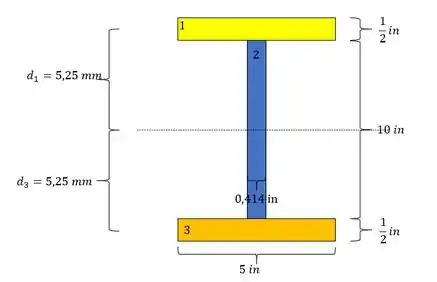
Além disso temos que:

A 1 = 5 × 1 2 = 2,5   i n 2

A 3 = 5 × 1 2 = 2,5   i n 2

I 1 = b h 3 12 = 5 × 1 2 3 12 = 0,0521   i n 4

I 2 = b h 3 12 = 0,414 × 1 0 3 12 = 34,5   i n 4

I 3 = b h 3 12 = 5 × 1 2 3 12 = 0,0521   i n 4

Assim a inercia da nossa seção vai ser dada por:

I = 0,0521 + 34,5 + 0,0521 + ( 2,5 × 5,25 2 + 2,5 × 5,25 2 )

I = 172,42   i n 4

Agora só precisamos determinar os valores de y, sendo assim teremos que ver o próximo passo.

Passo 3

Tendo o valor de y precisamos usar a tensão, sendo assim teremos que:

  • y - positivo e negativo

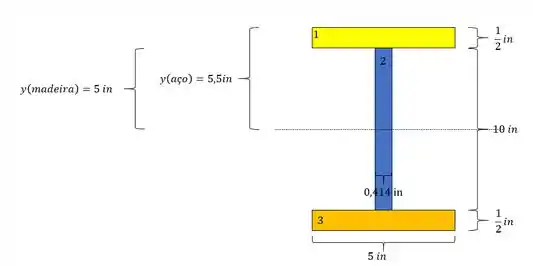
Calculando primeiro o latão:

σ a d m = 22 k s i = 22000   p s i = 22000 l b i n 2

y - - = - 5,5   i n

I = 172,42   i n 4

σ x = - M y I

Substituindo, teremos que:

22000 l b i n 2 = - M   .   ( - 5,5 ) i n 172,42   i n 4

M = 689680   l b ∙ i n = 689   k i p ∙ i n

E analisando agora o alumínio teremos que lembrar de acrescentar o fator de mudança   n :

σ a d m = 2000   p s i = 2000 l b i n 2

y - - = - 5   i n

I = 172,42   i n 4

σ x = - n M y I

Substituindo, teremos que:

2000 l b i n 2 = - 0,069 M   .   ( - 5 , 0 ) i n 172,42   i n 4

M = 999536   l b ∙ i n = 999,5   k i p ∙ i n

Como temos as tensões admissíveis, sabemos que ao momento que podemos aplicar será o menor dos que são dados acima, além dos mais, o maior momento dos dois irá romper a menor resistência, enquanto que o menor momento, garante a menor resistência e não afeta a maior, sendo assim teremos que:

M = 689   k i p ∙ i n

Resposta

M = 689   k i p ∙ i n

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Uma barra de aço e uma barra de alumínio são unidas para uma viga composta como o mostra a figura . Sabendo que a força cortante vertical na viga 17,8k N e que o módulo de elasticidade é 200G P a para
Determine a localização do centro de cisalhamento O de uma viga de paredes finas de espessura uniforme com a seção transversal mostrada.
Uma barra de aço e uma barra de alumínio são unidas para uma viga composta como o mostra a figura . Sabendo que a força cortante vertical na viga 17,8k N e que o módulo de elasticidade é 200G P a para
Determine a localização do centro de cisalhamento O de uma viga d paredes finas de espessura uniforme com a seção transversal mostrada.
Determine a localização do centro de cisalhamento O de uma viga d paredes finas de espessura uniforme com a seção transversal mostrada.