Enunciado
Mecânica e Resistência dos Materiais - Resistência dos materiais - 7ª Edição - Russel C. Hibbeler- Ed: 7º - Capítulo 9.Problemas - Ex. 25
25. Um bloco de madeira falhará, se a tensão de cisalhamento que age ao longo da fibra for . Se a tensão normal , determine a tensão de compressão necessária para provocar ruptura.
norma, determine a tensão de compressão
Passo 1
Fala! Da figura acima, tiramos que:
Já que temos tração.
Mas repara que as setinhas estão entrando, então essa tensão deve ser negativa. E:
Ele quer que a gente ache para que esse elemento tenha uma ruptura, sabendo que essa ruptura acontece por cisalhamento na direção do ângulo mostrado.
Vamos precisar relacionar com a tensão de cisalhamento do elemento rotacionado. Essa a gente considera que é a tensão que causa ruptura, então .
A gente precisa começar achando o ângulo de rotação para esse novo elemento. Vamos lá!
Passo 2
Para que o nosso cisalhamento esteja na direção das fibras, as faces do nosso elemento precisam estar paralelas as fibras. Na figura ele nos deu a orientção dessas fibras. Ficamos então com algo assim:
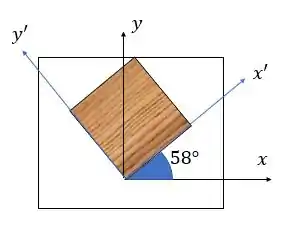
Dessa ilustração, podemos tirar o valor do ângulo , que vamos usar em nossos cálculos. Veja bem! O eixo , vai estar deslocado de um ângulo tal no sentido anti-horário, no valor de . Como é no sentido anti-horário, ele é positivo.
Agora, dado que a questão já nos fornece o valor da tensão de cisalhamento no elemento rotacionado, igual a , vamos usar a transformação de tensão cisalhante para encontrar .
Passo 3
A fórmula da tensão cisalhantes é dada por:
Substituímos, então os valores numéricos pertinentes a cada variável, para encontrar .