Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 85
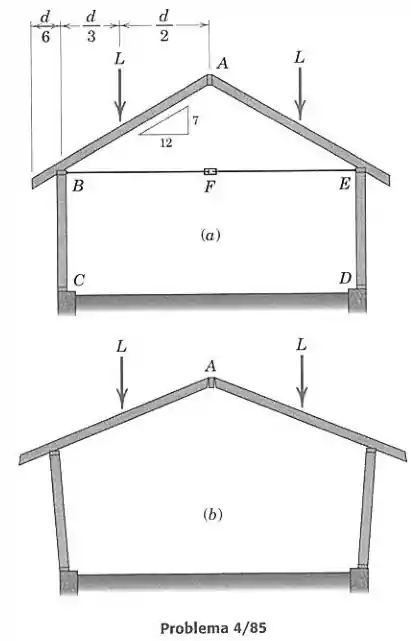
A figura ilustra um problema comum associado a estruturas simples. Sob os carregamentos , os caixilhos podem girar, a viga da cumeeira em A pode abaixar e as paredes e podem girar para fora, como mostrado na parte da figura. Esse fenômeno é às vezes observado claramente em estruturas antigas de madeira em fazendas, como uma deflexão central da viga da cumeeira quando vista de lado. Uma solução simples é mostrada na parte da figura. Uma corrente ou cabo é esticado entre as presilhas em e e o parafuso de ajuste é apertado até que uma força trativa adequada seja atingida, prevenindo, desta forma, a inclinação das paredes para fora. Para valores dados da dimensão e das cargas pontuais (que resultam das cargas distribuídas devidas aos pesos da viga da cumeeira, do telhado e de quaisquer cargas adicionais, tal como da neve), calcule a força trativa necessária para que não existam forças direcionadas para fora das paredes em e . Assuma que o apoio dos caixilhos na viga da cumeeira é puramente horizontal e que todas as juntas são livres para girar.
Passo 1
Vamos isolar o caixilho da esquerda, e observar as forças que atuam sobre ele. O problema nos diz que a força aplicada em pelo cabo é igual a e que a força no ponto causada pela viga é horizontal:
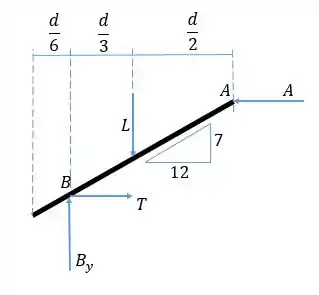
Passo 2
Achamos primeiro fazendo o equilíbrio das forças verticais, pois só temos essa incógnita nessa direção:
Agora fazendo o momento em torno de ser zero. A distância vertical de até é calculada assim:
Então:
Passando os termos com para a direita e dividindo tudo por :