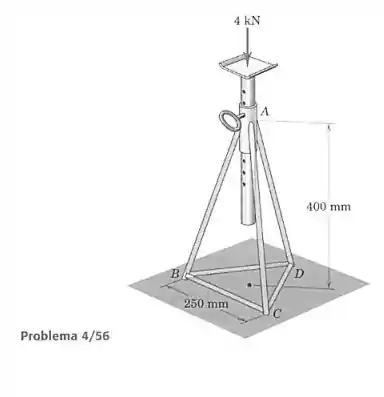
A base para um suporte para automóveis forma um triângulo equilátero com comprimento de aresta de 250 mm e está centrada em relação ao tubo cilíndrico . Modele a estrutura como se fosse composta de nós articulados e determine as forças nos elementos , e . Despreze quaisquer componentes de ação horizontal nos pés , e .

Como os apoios em , e só geram força vertical, podemos calcular essas forças facilmente, aplicando a equação de equilíbrio vertical da estrutura como um todo e com argumento de simetria:

Agora, se olharmos para o ponto , colocando o eixo em sendo o centroide do tiângulo , e o eixo vertical:

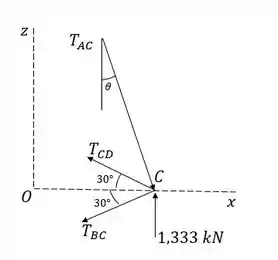
Pelo triângulo , temos:

Podemos fazer as equações de equilíbrio nos eixos e para encontrar

Vamos à equação em para encontrar :

Agora em temos:

Mas sabemos que , então:

Então, finalmente: