Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 4.6 - Ex. 102
Uma modificação feita no puxador do estrado do Prob. 4/101 é mostrada aqui. Para a mesma força líquida de 4 kN, como no Prob. 4/101, determine o módulo da força suportada pelo pino e as forças normais de aperto em e em .
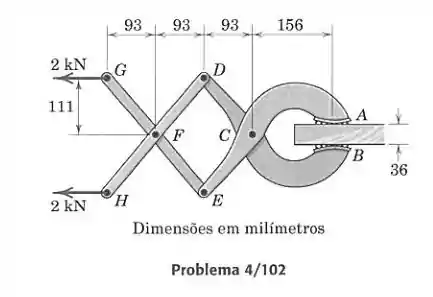
Passo 1
Agora como não é mais um elemento de duas forças(tem uma força atuando no meio da barra), a força feita em pelo elemento não tem mais a mesma direção da barra. Devemos isolar a barra e analisar as forças atuantes nela e descobrir os valores das forças em . A força em deve ser vertical, para garantir o equilíbrio do pino .
Passo 2
Primeiro fazendo o equilíbrio das forças no eixo encontramos :
Agora fazendo o equilíbrio das forças no eixo :
Então, finalmente fazemos o momento em torno de (escolhemos esse ponto por ter mais forças passando por ele):
Passo 3
Pronto, agora que temos e podemos olhar para o corpo e resolver as equações para ele como no problema 4/101. Devemos colocar essas duas forças no sentido contrário agora, pela lei da ação e reação:
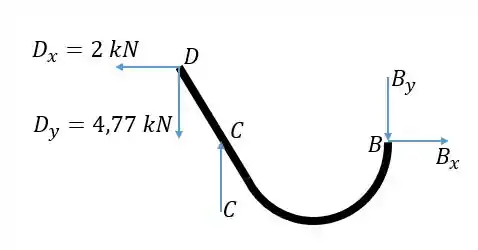
Passo 4
Conseguimos achar diretamente fazendo o momento em torno de :
Passo 5
Como só queremos a força vertical em e essa é a nossa única incógnita nessa direção, fazemos a soma das forças em ser zero:
Substituindo o valor de :
Pela simetria, temos também do outro lado