Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 2.Problemas - Ex. 98a
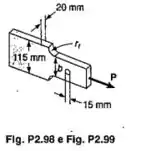
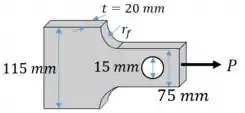
Uma força axial centrada P é aplicada à barra de aço mostrada. Sabendo-se que e , determinar:
- O maior valor admissível para P
- O menor valor permissível de para que no arredondamento a tensão normal admissível não seja excedida com a aplicação da carga P encontrada no item a)
Passo 1
A melhor forma de começar as questões de concentração de tensão é calculando os coeficientes de concentração de tensão.
Note que a questão tem dois concentradores: um furo e um arredondamento. Porém, como não sabemos o raio do arredondamento, vamos desconsiderá-lo.
Vamos calcular a concentração de tensão no furo:
Logo, a concentração de tensão no furo é:
Passo 2
Vamos calcular a maior tensão possível no furo. Mas antes, calculamos a área de seção transversal na região do furo. Cuidado! Não esqueça de desconsiderar o tamanho do furo!
E calculamos a força:
Isolamos o
Logo:
Resposta
Exercícios de Livros Relacionados
Para a viga prismática mostrada, determinar a deflexão no ponto D .
Para a viga prismática mostrada, determinar a deflexão no ponto D .
Para a viga prismática mostrada, determinar a deflexão no ponto D .
Para a viga e carregamento mostrado, pede-se:calcular o trabalho realizado pelas cargas, enquanto elas são aplicadas sucessivamente na viga, usando as informações do Apêndice D ;calcular a energia de
Para a viga e carregamento mostrado, pede-se:calcular o trabalho realizado pelas cargas, enquanto elas são aplicadas sucessivamente na viga, usando as informações do Apêndice D ;calcular a energia de