Enunciado
Mecânica e Resistência dos Materiais - Beer - Resistência dos Materiais- Ed: 3º - Capítulo 10.Problemas - Ex. 105
Para a viga e carregamento mostrado, pede-se:
- calcular o trabalho realizado pelas cargas, enquanto elas são aplicadas sucessivamente na viga, usando as informações do Apêndice ;
- calcular a energia de deformação da viga, pelo método da Sec. 10.4, e mostrar que isto é igual ao trabalho obtido na parte a.
Passo 1
Fala, pessoa! Tudo bem? Se liga, eu tô com dificuldades para fazer um exercício de cálculo de trabalho realizado por forças sobre uma viga que se deforma. Preciso de ajuda! Eu escolho você pra me dar uma mãozinha!
Temos que calcular o trabalho de duas formas. Na forma (a), temos que calcular o trabalho , quando a força do ponto é aplicada primeiro. é aumentada até fazer o ponto se deslocar . Além disso, essa força faz o ponto se deslocar . Depois, a força do ponto é aplicada até fazer o ponto se deslocar mais . Essa força também faz o ponto se deslocar mais .
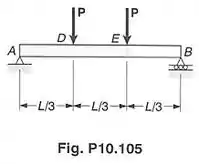
Na figura acima podemos ver como e variam conforme as deformações aumentam. Abaixo das curvas vermelhas podemos ver as áreas coloridas , e . O trabalho é a soma dessas áreas que estão sob as curvas das cargas.
Para calcular essas 3 áreas, precisamos saber quanto valem , , e . Para encontrar equações de , , e usamos o apêndice do livro. Faremos isso no próximo passo!
Passo 2
As equações de e são encontradas, quando consideramos que só existe um carregamento deformando a viga: a força . Nesse caso, o tipo de viga e carregamento é o tipo 5 da tabela desse apêndice , com o comprimento (do ponto ao ) do apêndice valendo e o comprimento (do ponto ao ) valendo . Logo:
Achamos fazendo o da equação do apêndice ser igual a .
Já as equações de e são obtidas, quando consideramos que só existe um carregamento deformando a viga: a força . Nesse caso, o tipo de viga e carregamento é o tipo 5 da tabela desse apêndice , com o comprimento (do ponto ao ) do apêndice valendo e o comprimento (do ponto ao ) valendo . Logo:
Achamos fazendo o da equação do apêndice ser igual a .
Com essas equações, somos capazes de achar todas as áreas no próximo passo.
Passo 3
Então é isso, galera. Só falta aprender a calcular as 3 áreas a partir de , , e que resolvemos a letra (a) da questão. Aprendemos isso, olhando para os gráficos do primeiro passo. No primeira figura vemos que é um triângulo de base e altura , é um retângulo de lados e e é um triângulo de base e altura . Por isso:
Substituindo essas áreas na equação de , achamos:
Aeee! Achamos a resposta da letra (a) da questão!
Vamos partir pra letra (b) agora!
Passo 4
Já falamos da forma (a) de se calcular o trabalho. Vamos entender qual seria a forma (b)!
A forma (b) de se calcular o trabalho é resolvendo a integral do momento fletor abaixo.
Para achar o trabalho , temos que resolver uma integral que tem o momento fletor da viga. Isso quer dizer que precisamos achar pra achar . No entanto, pra achar precisamos achar as forças de reação e nos apoios da viga! Isso é feito através do equilíbrio das forças em aplicadas sobre a viga.
Pela imagem, vemos que as forças e a viga são simétricas. Isso significa que a reação de um lado da viga é igual à reação do outro lado da viga. Além disso, pra escrever a equação de equilíbrio em , precisamos lembrar que as forças que apontam pra bai ganham um sinal de menos na frente.
Agora somos capazes de achar o momento fletor
Passo 5
Fazemos isso, dividindo a viga em duas partes (uma esquerda e outra direita). O será encontrando calculando o equilíbrio de momentos da parte esquerda da viga. tem três valores. Um, quando a parte esquerda da viga só inclui a força , outro quando essa parte só deixa a força de fora e o último, quando , e estão incluídos. O primeiro valor é calculado a partir da figura abaixo.
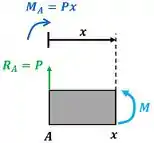
Faremos o equilíbrio dessa parte esquerda em relação ao ponto . A equação de equilíbrio de momentos diz que a soma dos momentos deve valer zero. Antes de escrever a equação, precisamos lembrar que os momentos que fazem a viga girar no sentido horário devem ganhar um sinal de menos na frente.
Conseguimos achar um valor para , mas tem um segundo valor. Quando a parte esquerda da viga inclui a força , esse momento fletor passa a ter outro valor.
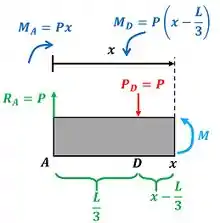
Só falta achar o terceiro valor de para calcular ! Ele é encontrado, quando fazemos o equilíbrio de momentos da parte esquerda viga e essa parte esquerda inclui as forças , e .
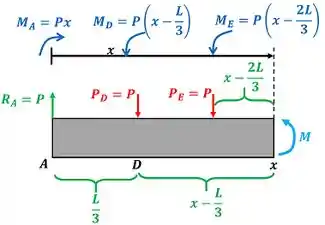
Pronto, com os dois valores de estamos aptos a encontrar !
Passo 6
tem três valores. Um quando vale entre e e outro, quando vale entre e e o último, quando está entre e
Por isso, para substituir na integral que calcula , precisamos separar a integral em três. Uma que vai de a para o primeiro valor de e outra que vai de a para o segundo valor de e a última que vai de a pro terceiro valor de .
Substituindo os valores de nas integrais corretas, achamos:
Colocando as constantes para fora da integral, achamos:
Uhuuul! Achamos a letra (b) da questão! Arrasamos!