Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 47
47. A força cria um momento em relação ao ponto O de . Se a força passa por um ponto tendo uma coordenada de , determine as coordenadas e do ponto. Além disso, observando que , determine a distância do ponto O à linha de ação de .
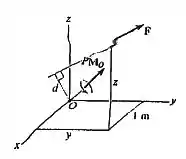
Passo 1
Para achar o resultado que o enunciado pede, vamos usar a forma de calcular o momento das forças usando o produto vetorial que é dado da seguinte maneira:
Onde:
representam as coordenadas do vetor que vai da origem da rotação até o ponto de aplicação da força;
são as componentes da força aplicada.
O enunciado já nos forneceu o (), agora só basta achar as outras componentes, para isso abrimos essa expressão acima com o que nos foi fornecido e assim descobrindo o valor das outras componentes de .
Passo 2
Vamos abrir a conta acima com o que temos então.
Então temos que:
Passo 3
Resolvendo esse pequeno sistema.
Assim, encontramos:
Passo 4
Agora para achar temos a seguinte fórmula:
Mas para usar essa fórmula precisamos usar os valores em módulo dos vetores que temos da força e do momento.
Então vamos calcular primeiro o módulo do vetor momento.
Agora vamos calcular o módulo do vetor força.
Assim usando a fórmula mencionada acima, temos:
Resposta
Assim, temos que: