Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 4.Problemas - Ex. 31

A barra no mecanismo de controle de potência de um jato comercial esta sujeita a uma força de 80   N . Determine o momento dessa fora em relação ao mancal em A .

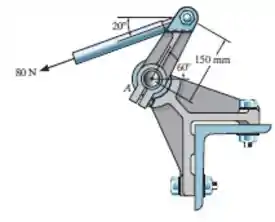
Passo 1

Temos uma alavanca e temos que determinar o momento nela.

Vamos simplificar o desenho para facilitar o entendimento:

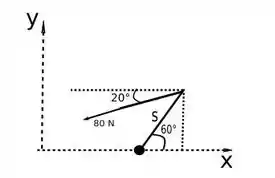
Temos o vetor força de 80   N e nossa haste S . Assim, vamos decompor a força e aplicar as equações da estática.

Passo 2

Note que podemos decompor o nosso vetor força nas componentes x e y e também poderemos decompor nossa haste S . Ficará desta forma:

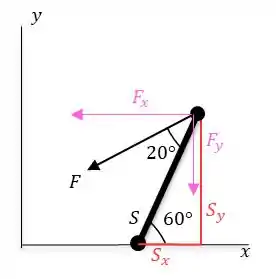
O que está em rosa é nossa força F e sua coordenadas x   e   y e oque está em vermelho o mesmo para S .

Passo 3

Após decompor os vetores, note que teremos dois tipos de momentos aqui neste eixo, teremos um momento no sentido anti-horário, causado pelos seguintes componentes:

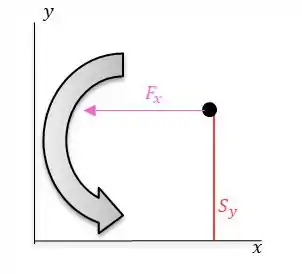
E teremos outro momento, no sentido horário, causado pelos seguintes componentes:

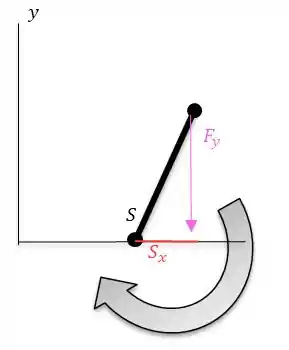
Passo 4

Agora que sabemos quais momentos existe nesta haste, vamos determinar este momento:

Considerando a rotação no sentido anti-horário como positivo, temos:

M A = F x ∙ S y - F y ∙ S x

Temos nosso momento, falta determinar estes componentes.

Passo 5

Determinando as componentes da força, temos o seguinte triângulo retângulo:

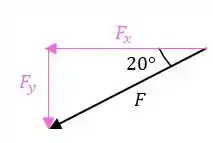
Aplicando seno, temos:

s e n   20 ° = F y F

F y = F ∙ s e n   20 °

Aplicando cosseno, temos:

cos ⁡ 20 ° = F x F

F x = F ∙ cos ⁡ 20 °

Passo 6

Determinando as componentes da haste, temos o seguinte triângulo retângulo:

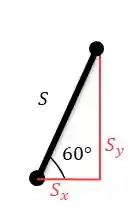
Aplicando seno, temos:

s e n   60 ° = S y S

S y = S ∙ s e n   60 °

Aplicando cosseno, temos:

cos ⁡ 60 ° = S x S

S x = S ∙ cos ⁡ 60 °

Passo 7

Retomando o cálculo do momento, temos:

M A = F x ∙ S y - F y ∙ S x

Substituindo os componentes que acabamos de calcular:

M A = F ∙ cos ⁡ 20 ° ∙ S ∙ s e n   60 ° - ( F ∙ s e n   20 ° ∙ S ∙ cos ⁡ 60 ° )

Substituindo a F = 80   N , S = 150   m m = 150 ∙ 10 - 3 m , multiplicando S por 10 - 3 para as unidades irem para metros e por final jogando os dados na calculadora, temos:

M A = 80 ∙ cos ⁡ 20 ° ∙ 0,150 ∙ s e n   60 ° - ( 80 ∙ s e n   20 ° ∙ 0,150 ∙ cos ⁡ 60 ° )

M A = 9,77 - 2,05

M A = 7,71   N ∙ m

Resposta

M A = 7,71   N ∙ m

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Determine o momento da força F em relação ao ponto A como uma função de θ . Represente os resultados de M (ordenada) em função de θ (abscissa) para ( 0 ° ≤ θ ≤ 180 ° ) .
Determine o ângulo θ ( 0 ° ≤ θ ≤ 180 ° ) da força F de modo que ela produza um momento máximo e um momento mínimo em relação ao ponto A . Além disso, quais são as intensidades desses momentos máximo e
Determine o momento produzido pela força F em relação ao ponto A em função do ângulo θ . Construa o gráfico de M A em função de θ , onde ( 0 ° ≤ θ ≤ 180 ° ) .
34. A fim de manter o carrinho de mão na posição indicada, a força F de produzir um momento anti-horário de 200N ⋅ m em relação a o eixo A. Determine a intensidade necessária da força F .