Enunciado

Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 46

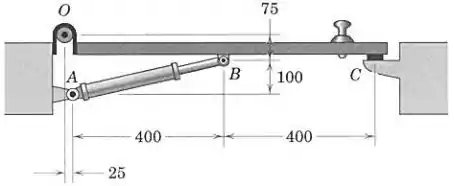
A força exercida pelo amortecedor sobre a porta vale e está direcionada ao longo da linha . Esta força tende a manter a porta fechada. Calcule o momento desta força em relação à dobradiça . Que força , normal ao plano da porta, deve ser exercida sobre a porta pelo batente em , de modo que o momento combinado das duas forças em relação a seja zero?

Passo 1

Galera, como a força de está direcionada ao longo da linha , podemos decompô-la em e , conforme mostra a figura a seguir:

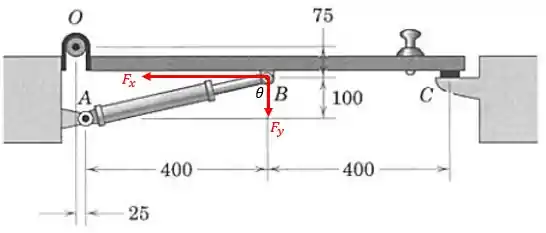
Então, o momento da força exercida pelo amortecedor em relação a será a soma dos momentos das duas componentes em relação a , no sentido horário (negativo):

Passo 2

Para que o momento em relação a se anule, precisamos de uma força atuando em para cima, de modo que seja produzido um momento no sentido anti-horário por essa força:

Resposta

(sentido horário)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

A força de 70 N age na extremidade do tubo em B. Determine os ângulos u (0° ≤ u ≤ 180°) da força que produzirão os momentos máximo e mínimo em relação ao ponto A. Quais são as intensidades desses mome

O elemento BC conectado à chave inglesa é usado para aumentar o seu braço de alavanca, conforme mostra a figura. Se um momento em sentido horário MA = 120 N  m é necessário para apertar o parafuso em

Se a força F = 100 N, determine o ângulo θ( 0 ≤ θ ≤ 90 ° ) , de modo que a força desenvolva um momento em sentido horário em relação ao ponto O de 20 N . m.

Determine a intensidade da força F que deverá ser aplicada na extremidade da alavanca, de modo que essa força crie um momento em sentido horário de 15 N . m em relação ao ponto O quando θ = 30 ° .

Determine a intensidade e o sentido direcional da força em A em relação ao ponto P .