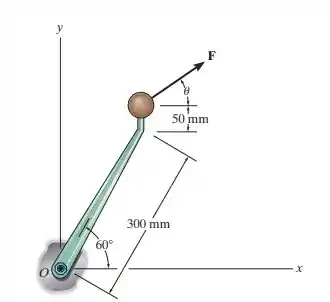
Se a força F = 100 N, determine o ângulo , de modo que a força desenvolva um momento em sentido horário em relação ao ponto O de 20 N . m.
Passo 1
Oi oi, meu xuxuzinho!! Tudo bem com você?? Como está com essa pandemia?? Preparado para voltar?? Então vamos lá Vamos analisar o que a nossa questão nos pede e matar essa em 10 minutos?? Bora. Bom, nosso enunciado nos pede para analisarmos a figura e dizermos qual a força a partir do eixo. Parece muita coisa, mas é tranquilo. Partiu??
Passo 2
Ok, nosso primeiro passo vai ser lembrar que, numa determinação de momento, cortante e normal, o cortante é positivo pela direita se ele for para baixo, e que a força aplicada deve ser sempre perpendicular à distância para sabermos o momento.
Quando se analisa o momento, ele é positivo toda vez que estiver girando no sentido anti-horário. Como a gente sabe disso?? Basta usar a regra da mão direita.
Redesenhando o diagrama, temos:
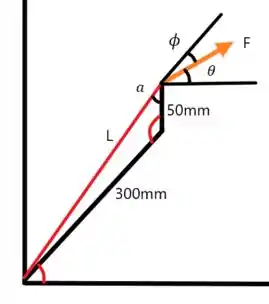
O ângulo na junta da alavanca é:
Aplicando a lei dos cossenos no ponto da junção da alavanca, temos:
Dessa forma, o ângulo entre e é:
Agora calculando o ângulo pela regra do cosseno novamente, temos:
Pela figura do diagrama redesenhado, temos que:
Logo:
Eaii?? Chegou bem até aqui??