Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia: Estática Volume 1 - 6ª Edição - James L. Meriam, L. Glenn Kraige- Ed: 6º - Capítulo 2.4 - Ex. 48
Calcule o momento da força de em relação ao ponto usando três métodos escalares e um método vetorial.
Passo 1
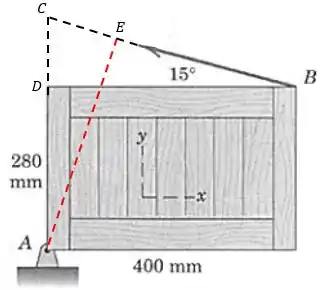
Podemos decompor a força de em uma componente horizontal e uma componente vertical , com ambas produzindo momento em relação a no sentido anti-horário (positivo):
Passo 2
Ou método para calcular o momento em torno de é multiplicar a força pela distância entre a linha de ação da força e o ponto . Essa distância será , de acordo com a figura:
Então,
Passo 3
Mais um método escalar é considerar a força como aplicada em , de modo que só precisamos multiplicar a força componente normal a e a distância :
Passo 4
Por último, podemos usar a fórmula vetorial:
Resposta
(sentido anti-horário)
Exercícios de Livros Relacionados
A grua pode ser ajustada para qualquer ângulo 0 ° ≤ θ ≤ 90 ° e qualquer extensão 0 ≤ x ≤ 5m . Para uma massa suspensa de 120k g , determine o momento desenvolvido em A em função de x e θ . Que valores
O cabo de reboque exerce uma força P = 6k N na extremidade da lança do guindaste de 8m de comprimento. Se x = 10m , determine a posição θ da lança para que essa força crie um momento máximo em relação
Determine a intensidade e o sentido direcional da força em A em relação ao ponto O .
Determine o momento produzido por cada força em relação ao ponto A.
O cabo de reboque exerce uma força P = 6k N na extremidade da lança do guindaste de 8m de comprimento. Se θ = 30 ° , determine o posicionamento x do gancho em B para que essa força crie um momento máx