Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 14ª Edição - Russel C. Hibbeler- Ed: 14º - Capítulo 7.Problemas - Ex. 114
Se a força de reboque horizontal for e a corrente tem uma massa por unidade de comprimento de , determine a flecha máxima . Despreze o efeito da flutuação da água sobre a corrente. Os barcos estão parados.
Passo 1
O problema quer que a gente encontre a tração máxima no cabo e comprimento do cabo entre e .
Vamos começar fazendo um diagrama de corpo livre, assim:
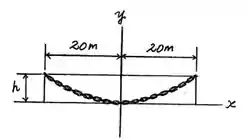
Onde o carregamento pode ser descrito como:
Você notou que estava em massa? A gente precisa do peso, por isso eu multipliquei pela gravidade aqui.
Enquanto que já sabemos que:
Passo 2
Nós notamos que na figura do problema, é o ponto mais baixo do cabo, vamos pegar a segunda derivada da equação do cabo, logo:
Se nós consideramos , então , logo:
E integrando isso:
Vamos encontrar , pra isso a gente usa a condição inicial, de que na origem, e então:
Logo é igual a .
Ficamos com:
Agora, vamos dar uma ajeitada e tentar simplicar isso, calma, eu sei que parece muito estranho:
Agora lembra que , aí ficamos com:
Integrando novamente para encontrar a função não derivada:
Aplicando a condição inicial para encontrarmos , encontramos que:
Logo, ficamos com:
Passo 3
E por fim, para descobrir , basta calcular a função, para quando :
E obtemos como resposta: