Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 93
Determine a força necessária para manter o cabo na posição mostrada, ou seja, de modo que o segmento permaneça horizontal. Além disso, calcule a flecha e a tração máxima no cabo.
Passo 1
O problema quer que a gente encontre a força , aa flecha e a tração máxima no cabo.
A gente vai começar analisando a junta :
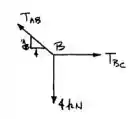
No eixo fica:
Assim, encontramos:
Passo 2
Então vamos analisar as forças da junta , assim:
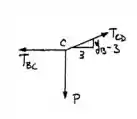
Combinamos as duas e simplificamos:
Passo 3
Fazendo o mesmo na junta , temos:
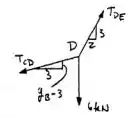
E usando o sistema de equações:
E temos:
Por fim, com todas as equações e informações que temos, encontramos:
Resposta
Exercícios de Livros Relacionados
Determine a força normal interna, o esforço cortante e o momento no ponto C da viga com apoio simples.
Determine a força normal interna, o esforço cortante e o momento no ponto C da viga simplesmente apoiada. O ponto C está localizado à direita do momento de binário de 2,5k N ∙ m .
Determine a força normal interna, o esforço cortante e o momento nos pontos E e F da viga.
Determine a força normal e o esforço cortante internos, e o momento nos pontos C e D da viga. Assuma que o apoio em B seja um rolete. O ponto C está localizado logo à direita da carga de 40k N .
Construa os diagramas de cortante e de momento para a viga, que sustenta a carga uniforme de 500 N por metro de comprimento da viga, distribuída ao longo da seção média. Determine o momento fletor máx