Enunciado
Mecânica e Resistência dos Materiais - Mecânica para Engenharia Estática - 12ª Edição - Russel C. Hibbeler- Ed: 12º - Capítulo 7.Problemas - Ex. 91
Os segmentos de cabo suportam a carga mostrada. Determine a distância horizontal a partir da força até o ponto . Faça .
Passo 1
O problema quer que a gente encontre a distância .
A gente vai começar calculando o momento em , que é:
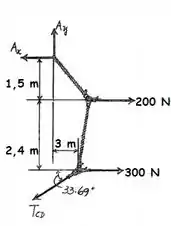
Agora, vamos analisar as forças, primeiro no eixo :
No eixo fica:
Passo 2
Então vamos analisar as forças da junta , assim:
Resolvendo o sistema:
A gente obtem:
Passo 3
Finalmente, calculamos a distância :
Resposta
Exercícios de Livros Relacionados
Determine a força normal, o esforço cortante e o momento no ponto C .
Determine a força normal, o esforço cortante e o momento no ponto C .
Determine a força normal, o esforço cortante e o momento no ponto C .
Determine a força normal interna, o esforço cortante e o momento no ponto C .
Determine o esforço cortante e o momento nos pontos C e D .